题目内容
18.所谓完全平方式,就是对于一个整式A,如果存在另一个整式B,使A=B2,则称A是完全平方式,例如:a4=(a2)2、4a2-4a+1=(2a-1)2.(1)下列各式中完全平方式的编号有①③④⑤;
①a6;②a2-ab+b2;③4a${\;}^{2}+2ab+\frac{1}{4}{b}^{2}$;④x2+4xy+4y2;⑤a2+a+0.25;⑥x2-6x-9.
(2)若x2+4xy+my2和x${\;}^{2}-nxy+\frac{1}{4}{y}^{2}$都是完全平方式,求(m-$\frac{1}{n}$)-1的值;
(3)多项式9x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是哪些?(请列出所有可能的情况,直接写答案)
分析 (1)利用完全平方公式的结构特征判断即可;
(2)利用完全平方公式的结构特征求出m与n的值,即可确定出原式的值;
(3)利用完全平方公式的结构特征判断即可.
解答 解:(1)①a6=(a2)3;②a2-ab+b2,不是完全平方式;③4a2+2ab+$\frac{1}{4}$b2=(2a+$\frac{1}{2}$b)2;④x2+4xy+4y2=(x+2y)2;⑤a2+a+0.25=(a+$\frac{1}{2}$)2;⑥x2-6x-9,不是完全平方式
各式中完全平方式的编号有①③④⑤;
故答案为:①③④⑤;
(2)∵x2+4xy+my2和x2-nxy+$\frac{1}{4}$y2都是完全平方式,
∴x2+4xy+my2=(x+$\sqrt{m}$y)2,x2-nxy+$\frac{1}{4}$y2=(x±$\frac{1}{2}$y)2,
∴m=4,n=±1,
当n=1时,原式=$\frac{1}{3}$;当n=-1时,原式=$\frac{1}{5}$;
(3)单项式可以为-1,-9x2,6x,-6x或$\frac{81}{4}$x4.
点评 此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
3.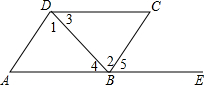 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠A+∠ABC=180° | C. | ∠A=∠5 | D. | ∠3=∠4 |
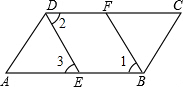 如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,DE∥FB.求证:AB∥DC.
如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,DE∥FB.求证:AB∥DC.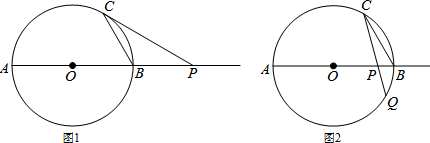
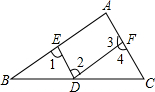 如图,下列条件:①∠1=∠2;②∠A=∠4;③∠1=∠4;④∠A+∠3=180°;⑤∠C=∠BDE,其中能判定AB∥DF的有( )
如图,下列条件:①∠1=∠2;②∠A=∠4;③∠1=∠4;④∠A+∠3=180°;⑤∠C=∠BDE,其中能判定AB∥DF的有( )