题目内容
6.阅读材料,解答问题:若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)下列各组二次函数中,是“同簇二次函数”的是③(填序号);
①y=x2+1与y=2x2;②y=x2+2x+2与y=2(x-1)2+1;③y=-x2-2x+3与y=-$\frac{1}{3}$(x+1)2+4
(2)已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式.
分析 (1)分别求得每一组两个函数的顶点即可判断;
(2)根据待定系数法求得y1的解析式,即可求得y1+y2=(2+a)x2+(b-4)x+8,根据同簇二次函数的概念得出2+a>0,-$\frac{b-4}{2(2+a)}$=1,$\frac{4(2+a)×8-(b-4)^{2}}{4(2+a)}$=1,即可求得a=5,b=-10,从而求得函数y2的表达式.
解答 解:(1)∵①y=x2+1与y=2x2开口都是向上,y=x2+1的顶点是(0,1),y=2x2的顶点是(0,0),故①不是;
∵②y=x2+2x+2与y=2(x-1)2+1开口都是向上,y=x2+2x+2=(x+1)2+1的顶点是(-1,1),y=2(x-1)2+1的顶点是(1,1),故②不是;
∵③y=-x2-2x+3与y=-$\frac{1}{3}$(x+1)2+4开口都是向下,顶点都是(-1,4),故②是;
故答案为③;
(2)∵二次函数y1=2x2-4mx+2m2+1的图象经过点A(1,1),
∴1=2×1-4m+2m2+1,
解得m=1,
∴y1=2x2-4x+3=2(x-1)2+1,则顶点坐标为(1,1),
∵y2=ax2+bx+5,
∴y1+y2=(2+a)x2+(b-4)x+8,
∵y1+y2与y1为“同簇二次函数”,
∴2+a>0,-$\frac{b-4}{2(2+a)}$=1,$\frac{4(2+a)×8-(b-4)^{2}}{4(2+a)}$=1,
解得a=5,b=-10,
∴函数y2的表达式为y2=5x2-10x+5.
点评 本题考查了二次函数的性质,掌握若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”的概念是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.若$\frac{2}{x-4}$有意义,则x的取值范围是( )
| A. | x>4 | B. | x≠4 | C. | x≥4 | D. | x<4 |
18.某水库养殖场连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(元)之间的函数关系式;(当天收入=日销售额-日捕捞成本)
(2)试说明(1)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | $5-\frac{x}{5}$ |
| 捕捞量(kg) | 950-10x |
(2)试说明(1)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
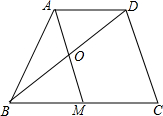 如图,在四边形ABCD中,点M是边BC的中点,AD∥BC,AM∥DC,AM与BD交于点O.求证:AO=OM.
如图,在四边形ABCD中,点M是边BC的中点,AD∥BC,AM∥DC,AM与BD交于点O.求证:AO=OM.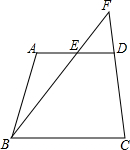 如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.
如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.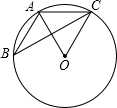 如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是60°.
如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是60°.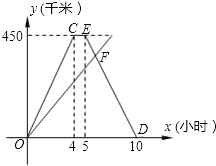 A、B两城间的公路长为450千米,甲、乙两车同时从A城出发沿这一公路驶向B城,甲车到达B城1小时后沿原路返回.如图是它们离A城的路程y(千米)与行驶时间 x(小时)之间的函数图象.
A、B两城间的公路长为450千米,甲、乙两车同时从A城出发沿这一公路驶向B城,甲车到达B城1小时后沿原路返回.如图是它们离A城的路程y(千米)与行驶时间 x(小时)之间的函数图象.