题目内容
9.计算(1)-32÷3+($\frac{1}{2}$-$\frac{2}{3}$)×12-(-1)2015
(2)170°÷6-6°36′42″×2.
分析 (1)先算乘方,再算乘除,最后算加减即可;
(2)先算乘除,再算加减即可.
解答 解:(1)原式=-9÷3+$\frac{1}{2}$×12-$\frac{2}{3}$×12+1
=-3+6-8+1
=-4;
(2)原式=28°20′-13°13′24″
=15°6′36″.
点评 本题考查的是有理数的混合运算,熟知有理数混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.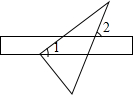 将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )
将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )
 将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )
将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )| A. | 90° | B. | 80° | C. | 75° | D. | 70° |
14.若$\frac{2}{x-4}$有意义,则x的取值范围是( )
| A. | x>4 | B. | x≠4 | C. | x≥4 | D. | x<4 |
18.某水库养殖场连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(元)之间的函数关系式;(当天收入=日销售额-日捕捞成本)
(2)试说明(1)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | $5-\frac{x}{5}$ |
| 捕捞量(kg) | 950-10x |
(2)试说明(1)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
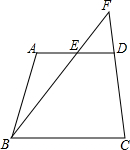 如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.
如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.