题目内容
8.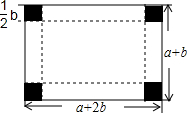 红枣丰收了,为了运输方便,小华的爸爸打算把一个长为(a+2b)cm、宽为(a+b)cm的长方形纸板制成一个有底无盖的盒子,在长方形纸板的四个角各截去一个边长为$\frac{1}{2}$bcm的小正方形,然后沿折线折起即可,如图所示,现将盒子的外表面贴上彩色花板.
红枣丰收了,为了运输方便,小华的爸爸打算把一个长为(a+2b)cm、宽为(a+b)cm的长方形纸板制成一个有底无盖的盒子,在长方形纸板的四个角各截去一个边长为$\frac{1}{2}$bcm的小正方形,然后沿折线折起即可,如图所示,现将盒子的外表面贴上彩色花板.(1)则至少需要彩纸的面积是多少?
(2)当a=8,b=6时,求至少需要彩纸的面积是多少?
分析 (1)根据图形表示出彩纸的面积即可;
(2)把a与b的值代入计算即可求出值.
解答 解:(1)根据题意得:(a+2b-b)(a+b-b)+b(a+2b-b)+b(a+b-b)=a2+ab+ab+b2+ab=a2+b2+3ab(cm2);
(2)当a=8,b=6时,原式=64+36+144=244(cm2).
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.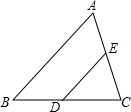 如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
 如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
20.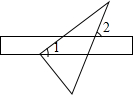 将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )
将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )
 将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )
将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )| A. | 90° | B. | 80° | C. | 75° | D. | 70° |
18.某水库养殖场连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(元)之间的函数关系式;(当天收入=日销售额-日捕捞成本)
(2)试说明(1)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | $5-\frac{x}{5}$ |
| 捕捞量(kg) | 950-10x |
(2)试说明(1)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
 ”可爱吧!表面能展开平面图形“
”可爱吧!表面能展开平面图形“ ”的是圆锥..
”的是圆锥..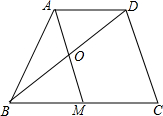 如图,在四边形ABCD中,点M是边BC的中点,AD∥BC,AM∥DC,AM与BD交于点O.求证:AO=OM.
如图,在四边形ABCD中,点M是边BC的中点,AD∥BC,AM∥DC,AM与BD交于点O.求证:AO=OM.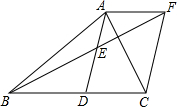 如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形.
如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形.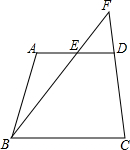 如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.
如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.