题目内容
12.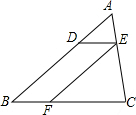 如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 2S1=S2 |
分析 根据已知条件得到四边形DBFE是平行四边形,由平行四边形的性质得到BD=EF,通过△ADE∽△ABC,得到$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{1}{3}$,推出DE=BF=$\frac{1}{2}$CF,然后根据图形的面积即可得到结论.
解答 证明:∵DE∥BC,EF∥AB
∴四边形DBFE是平行四边形,
∴BD=EF,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{1}{3}$,
∴DE=BF=$\frac{1}{2}$CF,
设DE与BC之间的距离为h,
∴S1=BF•h,S2=$\frac{1}{2}$CF•h,
∴S1=$\frac{1}{2}$CF•h,
∴S1=S2,
故选C.
点评 本题考查了平行四边形、三角形的面积公式,平行四边形的判定和性质、相似三角形的判定和性质、平行线分线段成比例定理的推论,熟练掌握相似三角形的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )
如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )
 如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )
如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\frac{4π}{3}$ | D. | $\frac{2\sqrt{3}π}{3}$ |
20.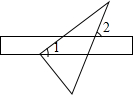 将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )
将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )
 将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )
将一块含60°角的直角三角板和直尺如图放置,使三角板的直角顶点落在直尺的一边上,若∠1=40°,则∠2的度数是( )| A. | 90° | B. | 80° | C. | 75° | D. | 70° |
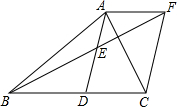 如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形.
如图,在△ABC中,AD是BC边的中线,E是AD的中点,过A点作AF∥BC交BE的延长线于点F,连结CF.求证:四边形ADCF是平行四边形. 如图,已知圆周角∠ACB的度数为100°,则圆周角∠D的度数等于80°.
如图,已知圆周角∠ACB的度数为100°,则圆周角∠D的度数等于80°.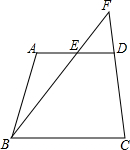 如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.
如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.