题目内容
2. 有一种足球是由32块黑白相间的牛皮缝制而成的(如图),黑皮可看作正五边形,白皮可看作正六边形.设白皮有x块,则黑皮有(32-x)块,要求出黑皮、白皮的块数,列出的方程是( )
有一种足球是由32块黑白相间的牛皮缝制而成的(如图),黑皮可看作正五边形,白皮可看作正六边形.设白皮有x块,则黑皮有(32-x)块,要求出黑皮、白皮的块数,列出的方程是( )| A. | 3x=32-x | B. | 3x=5(32-x) | C. | 5x=3(32-x ) | D. | 6x=32-x |
分析 因每块白皮有三条边和黑皮连在一起,所以黑皮的边数可以根据白皮的边数确定;另外黑皮的边数还可以根据一块黑皮有5条边,n块黑皮就有5n条边来确定,根据黑皮的边数一定,列方程即可.
解答 解:设白皮有x块,则黑皮有(32-x)块,依题意可列方程为:
3x=5(32-x).
故选B.
点评 本题考查了由实际问题抽象出一元一次方程,关键是理解题意,找到正确的等量关系.

练习册系列答案
相关题目
13.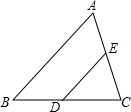 如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
 如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
10.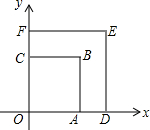 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )| A. | ($\sqrt{2},0$) | B. | ($\frac{3}{2},\frac{3}{2}$) | C. | ($\sqrt{2},\sqrt{2}$) | D. | (2,2) |
14.若$\frac{2}{x-4}$有意义,则x的取值范围是( )
| A. | x>4 | B. | x≠4 | C. | x≥4 | D. | x<4 |
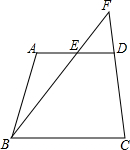 如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.
如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.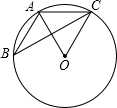 如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是60°.
如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是60°. 如图所示,AD=BC,试判断AB与CD的大小关系,并说明理由.
如图所示,AD=BC,试判断AB与CD的大小关系,并说明理由.