题目内容
7.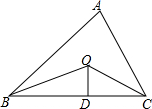 如图,已知△ABC的周长是22,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是多少?
如图,已知△ABC的周长是22,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是多少?
分析 根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等,从而可得到△ABC的面积等于周长的一半乘以OD,然后列式进行计算即可求解.
解答 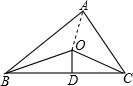 解:如图,连接OA,
解:如图,连接OA,
∵OB、OC分别平分∠ABC和∠ACB,
∴点O到AB、AC、BC的距离都相等,
∵△ABC的周长是22,OD⊥BC于D,且OD=3,
∴S△ABC=$\frac{1}{2}$×22×3=33.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,判断出三角形的面积与周长的关系是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
2. 如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )
如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )
 如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )
如图,将Rt△ABC,其中∠B=30°,∠C=90°,AC=1,绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么,点B所运动的路径长( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\frac{4π}{3}$ | D. | $\frac{2\sqrt{3}π}{3}$ |
 ”可爱吧!表面能展开平面图形“
”可爱吧!表面能展开平面图形“ ”的是圆锥..
”的是圆锥..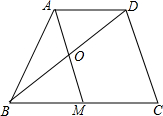 如图,在四边形ABCD中,点M是边BC的中点,AD∥BC,AM∥DC,AM与BD交于点O.求证:AO=OM.
如图,在四边形ABCD中,点M是边BC的中点,AD∥BC,AM∥DC,AM与BD交于点O.求证:AO=OM.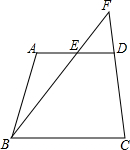 如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.
如图,在四边形ABCD中,AD∥BC,点E是边AO的中点,连接BE,BE的延长线交CD的延长线于点F,求证:$\frac{EF}{FB}=\frac{AE}{BC}$.