题目内容
2. 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )| A. | $\sqrt{41}$ | B. | $\sqrt{34}$ | C. | 8 | D. | 6 |
分析 首先延长CA,交⊙A于点F,易得∠BAF=∠DAE,由圆心角与弦的关系,可得BF=DE,由圆周角定理可得:∠CBF=90°,然后由勾股定理求得弦BC的长.
解答  解:延长CA,交⊙A于点F,
解:延长CA,交⊙A于点F,
∵∠BAC+∠BAF=180°,∠BAC+∠EAD=180°,
∴∠BAF=∠DAE,
∴BF=DE=6,
∵CF是直径,
∴∠ABF=90°,CF=2×5=10,
∴BC=$\sqrt{C{F}^{2}-B{F}^{2}}$=8.
故选C.
点评 此题考查了圆周角定理、圆心角与弦的关系以及勾股定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
13.已知关于x的方程x2-3mx+5m-2=0的一个根为x=2,且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 6或10 |
7.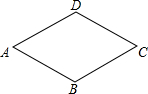 如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
 如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )| A. | 16 | B. | 16$\sqrt{2}$ | C. | 16$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
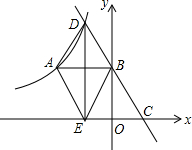 如图所示,在平面直角坐标系中,双曲线y=$\frac{k}{x}$(x<0)上有一点A(-2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.
如图所示,在平面直角坐标系中,双曲线y=$\frac{k}{x}$(x<0)上有一点A(-2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.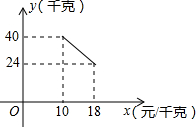 某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示,该经销商想要每天获得150元的销售利润,销售价应定为多少?列出关于x方程是(x-10)(-2x+60)=150(不需化简和解方程).
某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示,该经销商想要每天获得150元的销售利润,销售价应定为多少?列出关于x方程是(x-10)(-2x+60)=150(不需化简和解方程).