题目内容
17.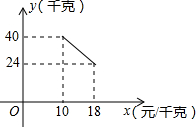 某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示,该经销商想要每天获得150元的销售利润,销售价应定为多少?列出关于x方程是(x-10)(-2x+60)=150(不需化简和解方程).
某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示,该经销商想要每天获得150元的销售利润,销售价应定为多少?列出关于x方程是(x-10)(-2x+60)=150(不需化简和解方程).
分析 设函数关系式y=kx+b,把(10,40),(18,24)代入求出k和b,然后用销售量×单件利润=总利润即可列出方程.
解答 解:设y与x之间的函数关系式y=kx+b,把(10,40),(18,24)代入得
$\left\{\begin{array}{l}{10k+b=40}\\{18k+b=24}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=60}\end{array}\right.$,
∴y与x之间的函数关系式y=-2x+60(10≤x≤18),
∴W=(x-10)(-2x+60),
当销售利润为150元时,可得:(x-10)(-2x+60)=150,
故答案为:(x-10)(-2x+60)=150.
点评 本题考查了函数的应用及由实际问题抽象出一元二次方程的知识,得到每天的销售利润的关系式是解决本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
7.如果x2-(m-1)x+1是一个完全平方式,则m的值为( )
| A. | -1 | B. | 1 | C. | -1或3 | D. | 1或3 |
5. 如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
 如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )| A. | 圆 | B. | 椭圆 | ||
| C. | 一般的平行四边形 | D. | 矩形 |
2. 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )| A. | $\sqrt{41}$ | B. | $\sqrt{34}$ | C. | 8 | D. | 6 |
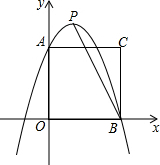 如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)
如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4) 如图是一个转盘,转一次指针指向灰色部分的概率是$\frac{1}{3}$.
如图是一个转盘,转一次指针指向灰色部分的概率是$\frac{1}{3}$.