题目内容
17.已知二次函数y1=ax2+4x+b与y2=bx2+4x+a都有最小值,记y1、y2的最小值分别为m、n.(1)若m+n=0,求证:对任意的实数x,都有y1+y2≥0;
(2)若m,n均为大于0,且mn=2,记M为m,n中的最大者,求M的最小值.
分析 (1)根据题意可以用用含a,b的代数式表示m、n,然后根据m+n=0,可以解答本题;
(2)根据题意可以用用含a,b的代数式表示m、n,然后根据mn=2,记M为m,n中的最大者,可以求得M的最小值.
解答 解:(1)∵y1=ax2+4x+b=a(x+$\frac{2}{a}$)2+$\frac{ab-4}{a}$,
∴m=$\frac{ab-4}{a}$,
∵y2=bx2+4x+a=b(x+$\frac{2}{b}$)2+$\frac{ab-4}{b}$,
∴n=$\frac{ab-4}{b}$,
∵m+n=0,
∴$\frac{ab-4}{a}$+$\frac{ab-4}{b}$=0,即(ab-4)($\frac{1}{a}+\frac{1}{b}$)=0,
∵a>0,b>0,
∴$\frac{1}{a}+\frac{1}{b}$>0,
∴ab-4=0,即ab=4,
∴m=n=0,
∵y1、y2的最小值分别为m、n,
∴y1+y2≥m+n=0,
∴y1+y2≥0;
(2))∵y1=ax2+4x+b=a(x+$\frac{2}{a}$)2+$\frac{ab-4}{a}$,
∴m=$\frac{ab-4}{a}$,
∵y2=bx2+4x+a=b(x+$\frac{2}{b}$)2+$\frac{ab-4}{b}$,
∴n=$\frac{ab-4}{b}$,
∵mn=2,
∴$\frac{ab-4}{a}$•$\frac{ab-4}{b}$=2,
解得,ab=2或ab=8,
∴$\left\{\begin{array}{l}{m=\frac{-2}{a}}\\{n=\frac{-2}{b}}\end{array}\right.$或$\left\{\begin{array}{l}{m=\frac{4}{a}}\\{n=\frac{4}{b}}\end{array}\right.$,
当$\left\{\begin{array}{l}{m=\frac{-2}{a}}\\{n=\frac{-2}{b}}\end{array}\right.$时,
若a>b,则m>n,M=$\frac{-2}{a}$,
若a<b,则m<n,M=$\frac{-2}{b}$;
当$\left\{\begin{array}{l}{m=\frac{4}{a}}\\{n=\frac{4}{b}}\end{array}\right.$,
若a>b,则m<n,M=$\frac{4}{b}$,
若a<b,则m>n,M=$\frac{4}{a}$;
由上可得,当a>b时,M的最小值是$\frac{-2}{a}$;
当a<b时,M的最小值是$\frac{-2}{b}$.
点评 本题考查二次函数的最值,解题的关键是明确题意,可以将函数的一般式化为顶点式,利用分类讨论的数学思想和数形结合的思想解答问题.

| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | 2 |
 如图,在矩形ABCD中,AB=5,BC=6,点E是AD上一点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠ADC的平分线上时,DA1=2$\sqrt{2}$.
如图,在矩形ABCD中,AB=5,BC=6,点E是AD上一点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠ADC的平分线上时,DA1=2$\sqrt{2}$. 如图,AD与BC交于点E,∠BAC=∠ACD=90°,∠B=45°,∠D=30°,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}}{3}$.
如图,AD与BC交于点E,∠BAC=∠ACD=90°,∠B=45°,∠D=30°,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}}{3}$.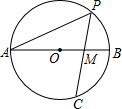 如图,在⊙O中,AB为直径,PC为弦,且PA=PC,PC交AB于M,若∠APC=45°,求$\frac{AM}{BM}$的值.
如图,在⊙O中,AB为直径,PC为弦,且PA=PC,PC交AB于M,若∠APC=45°,求$\frac{AM}{BM}$的值. 如图,△ABC是等边三角形,AB=2,D是边BC的中点,点P从点A出发,沿AB-BD以每秒1个单位长度的速度向终点D运动.同时点Q从点C出发,沿CA-AC以每秒1个单位长度的速度运动.当点P停止运动时,点Q也随之停止运动,设点P的运动时间为t(秒),△PQD的面积为S.
如图,△ABC是等边三角形,AB=2,D是边BC的中点,点P从点A出发,沿AB-BD以每秒1个单位长度的速度向终点D运动.同时点Q从点C出发,沿CA-AC以每秒1个单位长度的速度运动.当点P停止运动时,点Q也随之停止运动,设点P的运动时间为t(秒),△PQD的面积为S.