题目内容
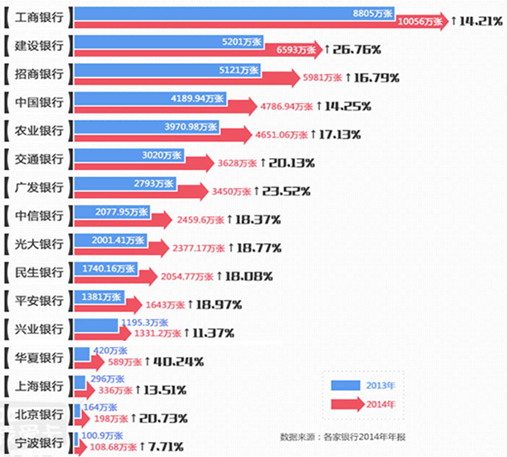
7．一座拱型桥，桥下水面宽度AB是16米，拱高CD是4米，大雨过后，桥下水面宽度EF是12米，求水面上涨了多少米？（1）若把它看作是抛物线的一部分，在坐标系中（如图1），可设抛物线的表达式为y=ax2+c，请你求出此时水面上涨了多少米？
（2）若把它看作是圆的一部分，则可构造图形（如图2），请你求出此时水面上涨了多少米？
分析 （1）根据题意知抛物线顶点坐标（0，4），设其顶点式y=ax2+4，将点A或点B坐标代入求得其解析式，再求当x=6时y的值即可得答案；
（2）由垂径定理知BC=$\frac{1}{2}$AB、PF=$\frac{1}{2}$EF，设⊙O半径为r，在RT△OBC中根据OB2=OC2+BC2求得r的值及OC的长，再在RT△OFP中根据OF2=PF2+OP2求得OP的长，由OP-OC可得答案．
解答 解：（1）由题意可知抛物线顶点为（0，4），
设抛物线解析式为：y=ax2+4，
将点B（8，0）代入，得：64a2+4=0，
解得：a=-$\frac{1}{16}$，
∴该抛物线解析式为：y=-$\frac{1}{16}$x2+4，
当x=6时，y=-$\frac{1}{16}$×36+4=$\frac{7}{4}$，
故水位上涨了$\frac{7}{4}$米；
（2）如图，连接OB、OF，记EF与OD交点为P，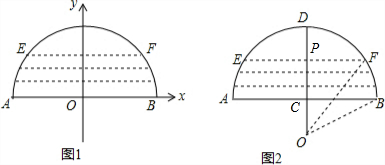
根据题意知，BC=$\frac{1}{2}$AB=8m，PF=$\frac{1}{2}$EF=6m，CD=4m，
设⊙O半径为r，则OC=r-4，
由OB2=OC2+BC2，可得r2=（r-4）2+82，
解得：r=10，
∴OC=6m，
在RT△OPF中，由OF2=PF2+OP2，得：102=62+OP2，
解得：OP=8m，
∴PC=OP-OC=8-6=2（m）
故此时水面上涨了2米．
点评 本题主要考查待定系数法求函数解析式及垂径定理、勾股定理的应用，根据不同条件设出合适的二次函数解析式是解决问题的关键．
练习册系列答案
相关题目
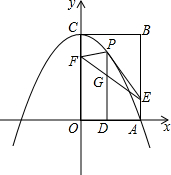如图，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A、C间的一个动点（含端点），过点P作PD⊥OA于点D，点E（8，2），F（0，6），连接PE、PF、EF．
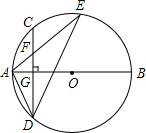如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足$\frac{CF}{FD}$=$\frac{1}{3}$，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3，给出下列结论：
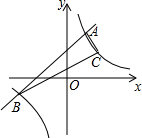已知一次函数y1=x+5的图象与反比例函数y2=$\frac{k}{x}$的图象交于A、B两点，已知点A的横坐标为1．
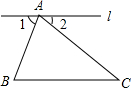如图，点A在直线l上，如果∠B=75°，∠C=43°，若l∥BC，则∠BAC=62°．
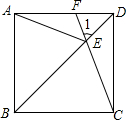如图，在正方形ABCD中，E是对角线BD上任意一点（BE＞DE），CE的延长线交AD于点F，连接AE．