题目内容

6．在Rt△ABC中，∠C=90°，BC=3，AC=4，那么cosA=$\frac{4}{5}$．

分析 先利用勾股定理列式求出斜边AB的长，再根据锐角的余弦等于邻边比斜边列式即可．

解答 解：由勾股定理得，AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5，
所以cosA=$\frac{AC}{AB}$=$\frac{4}{5}$．
故答案为：$\frac{4}{5}$．

点评 本题考查了锐角三角函数的定义，勾股定理，难点在于求出斜边的长度，作出图形更形象直观．

练习册系列答案
相关题目
14．若关于x的一元二次方程x2-2（2-k）x+k2+12=0有实数根α、β．
（1）求实数k的取值范围；
（2）若$\frac{α}{β-1}$+$\frac{β}{α-1}$=4，求k的值．
17．已知二次函数y1=ax2+4x+b与y2=bx2+4x+a都有最小值，记y1、y2的最小值分别为m、n．
（1）若m+n=0，求证：对任意的实数x，都有y1+y2≥0；
（2）若m，n均为大于0，且mn=2，记M为m，n中的最大者，求M的最小值．
14．如图1，在平面直角坐标系中，抛物线y=$\frac{1}{2}{x}^{2}$-2x-6与x轴交于A．B两点（点A在点B左侧）．与y轴交于点T，抛物线顶点为C．
（1）求四边形OTCB的面积；
（2）如图2，抛物线的对称轴与x轴交于点D．线段EF与PQ长度均为2，线段EF在线段DB上运动．线段PQ在y轴上运动，EE′，FF′分别垂直于x轴，交抛物线于点E′，F′，交BC于点M，N．请求出ME′+NF′的最大值，并求当ME′+NF′值最大时，四边形PNMQ周长的最小值；
（3）如图3，连接AT，将△AOT沿x轴向右平移得到△A′O′T′，当T′与直线BC的距离为$\frac{\sqrt{5}}{5}$时，求△A′O′T′与△BCD的重叠部分面积．
1．如图，在平面直角坐标系中，点A（0，n），B（m，0）中的m，n是方程组$\left\{\begin{array}{l}{m+n=-2}\\{m-n=-14}\end{array}\right.$的解，点C在x轴的正半轴上，且OA=2OC，AB=10，过点A作AD⊥y轴，过点C作CD⊥AD于点D，动点P从点D出发，以每秒2个单位长度的速度在射线DA上运动，同时另一动点Q从点B出发向终点A运动，速度是每秒3个单位长度，一点停止运动另一点也停止，设运动时间为t秒．
（1）求出点A、B、C的坐标；
（2）连接PC，请用含t的关系式来表示△PAC的面积S；
（3）是否存在某一时刻t，使△PAC的面积等于△BOQ面积的一半？若存在请求出t值，若不存在请说明理由．
11．已知一次函数y=（1-3m）x+1，若y随x的增大而减小，则m的取值范围是（　　）
A．m＜$\frac{1}{3}$B．m＜-$\frac{1}{3}$C．m＞$\frac{1}{3}$D．m＞-$\frac{1}{3}$
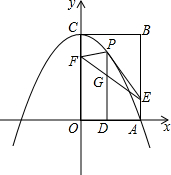18．如图，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A、C间的一个动点（含端点），过点P作PD⊥OA于点D，点E（8，2），F（0，6），连接PE、PF、EF．
（1）直接写出抛物线和直线EF的解析式．
（2）小明探究点P的位置发现：当点P与点A或点C重合时，PD与PF的和为定值，进而猜想：对于任意一点P，PD与PF的和为定值，请你判断该猜想是否正确，并说明理由．
（3）小明进一步探究得出结论：
①使得PD-PE最大的点P是否存在？若存在求出点P的坐标，否则说明理由．
②若将“使△PEF得面积为整数”的点P记作“好点”，且存在多个“好点”，请直接写出所有“好点”的个数，求出使得△PEF的面积最大的好点P的坐标．
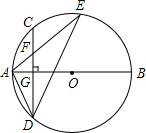15．如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足$\frac{CF}{FD}$=$\frac{1}{3}$，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3，给出下列结论：
①△ADF∽△AED；②FG=3；③tan∠E=$\frac{\sqrt{5}}{2}$；④S△ADE=6$\sqrt{5}$．
其中正确的有个数是（　　）
A．1个B．2个C．3个D．4个
1．若a，b为实数，且|a+1|+$\sqrt{b-1}$=0，则（ab）2014的值为1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网