题目内容
2.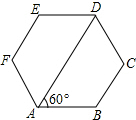 如图,六边形ABCDEF的各个内角都相等,且∠DAB=60°.
如图,六边形ABCDEF的各个内角都相等,且∠DAB=60°.(1)求∠E的度数.
(2)在不添加任何字母和辅助线的情况下,直接写出图中所有平行线段.
(3)选择(2)中的一组平行线段,为其成立说明理由.
分析 (1)利用多边形内角和公式进行计算即可;
(2)根据(1)的结论可以得到图中有EF∥BC,AF∥CD,EF∥AD,BC∥AD;
(3)由于六边形的内角和为720°,然后利用六边形ABCDEF的内角都相等得到每个内角的度数为120°,而∠DAB=60°,四边形ABCD的内角和为360°,由此即可分别求出∠CDA和∠EDA,最后利用平行线的判定方法即可求解.
解答 (1)解:∵六边形ABCDEF的各个内角都相等,
∴∠E=$\frac{180°(6-2)}{6}$=120°;
(2)解:EF∥BC,AF∥CD,EF∥AD,BC∥AD.
(3)证明:六边形的内角和为:(6-2)×180°=720°.
∵六边形ABCDEF的内角都相等,
∴每个内角的度数为:720°÷6=120°.
又∵∠DAB=60°,四边形ABCD的内角和为360°,
∴∠CDA=360°-∠DAB-∠B-∠C=360°-60°-120°-120°=60°,
∴∠EDA=120°-∠CDA=120°-60°=60°,
∴∠EDA=∠DAB=60°,
∴AB∥DE(内错角相等,两直线平行).
点评 此题主要考查了平行线的判定及多边形的内角和定理,关键是掌握多边形内角和公式(n-2)•180°(n≥3)且n为整数),掌握平行线的判定定理.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
13.一组数据1,3,2,5,2,a的众数是a,这组数据的中位数是( )
| A. | 3 | B. | 2 | C. | 1.5 | D. | 2.5 |
10.下列各式由左边到右边的变形,是因式分解的是( )
| A. | x2-2x+1=(x-1)2 | B. | (x+1)(x-1)=x2-1 | C. | x2-2x+1=x(x-2)+1 | D. | (x+3)(x-2)=x2+x-6 |
12.某校运动员进行分组训练,若每组5人,余2人,若每组6人,则缺3人,设运动员人数为x人,组数为y,则根据题意所列方程组为( )
| A. | $\left\{\begin{array}{l}{5y=x+2}\\{6x+3=x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5y=x+2}\\{6y-3=x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{5y=x-2}\\{6y=x+3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5y=x-2}\\{6y=x-3}\end{array}\right.$ |
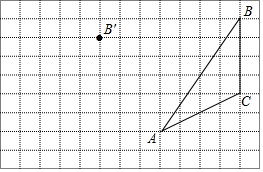 如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.
如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.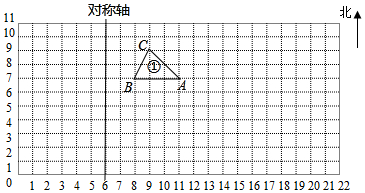 如图每个小正方形的边长表示1厘米,请按要求画图形.
如图每个小正方形的边长表示1厘米,请按要求画图形.