题目内容
18.A、B两地相距11km,甲,乙两人分别从A,B两地同时出发,相向而行,相遇时,甲距B地还有5km,相遇后,两人继续前进,且甲到达B地的时间比乙到达A地的时间早22min,求甲、乙两人的速度.分析 根据题意可得相遇时,甲走了6千米,乙走了5千米,相遇后,甲又走5km,乙走了6千米,设甲的速度为xkm/h,则乙的速度为$\frac{5}{\frac{6}{x}}$=$\frac{5}{6}$xkm/h,根据题意可得等量关系:甲走5千米的时间-乙走6千米的时间=22分钟,根据等量关系列出方程,再解即可.
解答 解:设甲的速度为xkm/h,则乙的速度为$\frac{5}{\frac{6}{x}}$=$\frac{5}{6}$xkm/h,由题意得:
$\frac{6}{\frac{5x}{6}}$-$\frac{5}{x}$=$\frac{22}{60}$,
解得:x=6,
经检验:x=6是原分式方程的解,
则乙的速度为$\frac{5}{6}$×6=5(km/h),
答:甲的速度为6km/h,则乙的速度为5km/h.
点评 此题主要考查了分式方程的应用,关键是正确理解题意,设出未知数,表示出甲和乙的速度,再找出题目中的等量关系,列出方程,注意分式方程必须检验.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
6.关于函数y=-$\frac{2}{3}$x2的性质描述错误的是( )
| A. | 它的图象关于y轴对称 | |
| B. | 该抛物线开口向下 | |
| C. | 原点是该抛物线上的最高点 | |
| D. | 当x为任意实数时,函数值y总是负数 |
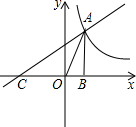 如图,在平面直角坐标系中,直线$y=x+\frac{k}{2}$与双曲线$y=\frac{k}{x}$在第一象限交于点A,与x轴交于点C,AB⊥x轴,垂足为B,此时点B(1,0).求:
如图,在平面直角坐标系中,直线$y=x+\frac{k}{2}$与双曲线$y=\frac{k}{x}$在第一象限交于点A,与x轴交于点C,AB⊥x轴,垂足为B,此时点B(1,0).求: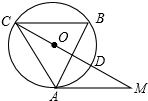 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.
