题目内容
1.解下列方程:(1)x2-2x-5=0;
(2)(x-3)2+2(x-3)=0.
分析 (1)公式法求解可得;
(2)因式分解法求解可得.
解答 解:(1)∵a=1,b=-2,c=-5,
∴△=4-4×1×(-5)=24>0,
∴x=$\frac{2±2\sqrt{6}}{2}$=1$±\sqrt{6}$;
(2)∵(x-3)2+2(x-3)=0,
∴(x-3)(x-3+2)=0,即(x-3)(x-1)=0,
则x-3=0或x-1=0,
解得:x=3或x=1.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
11.某农场引进一批新稻种,在播种前做了五次发芽实验,每次任取800粒稻种进行实验.实验的结果如下表所示:
在与实验条件相同的情况下,估计种一粒这样的稻种发芽的概率为0.95(精确到0.01);如果该农场播种了此稻种2万粒,那么能发芽的大约有1.9万粒.
| 实验的稻种数n∕粒 | 800 | 800 | 800 | 800 | 800 |
| 发芽的稻种数m∕粒 | 763 | 757 | 761 | 760 | 758 |
| 发芽的频率$\frac{m}{n}$ | 0.954 | 0.946 | 0.951 | 0.950 | 0.948 |
6. 如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
 如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )| A. | $\frac{4}{3}$π-$\sqrt{3}$ | B. | 2π-2$\sqrt{3}$ | C. | $\frac{2}{3}$π-$\sqrt{3}$ | D. | $\frac{1}{3}$π |
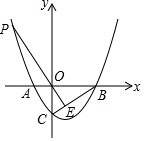 如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,点P为第二象限的抛物线上一点,且线PO交BC于E.
如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,点P为第二象限的抛物线上一点,且线PO交BC于E.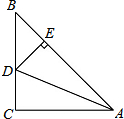 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是6,则AB,AC的长.
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是6,则AB,AC的长.