题目内容
2. 如图,已知∠1=70°,∠2=110°,那么AB与CD平行吗?为什么?
如图,已知∠1=70°,∠2=110°,那么AB与CD平行吗?为什么?
分析 利用互补的性质,先求出∠3,根据∠1和它的同位角∠3相等即可证明.
解答  解:AB与CD平行.
解:AB与CD平行.
理由:∵∠2+∠3=180°,∠2=110°(已知),
∴∠3=70°(等式的性质).
∵∠1=70°(已知),
∴∠1=∠3(等量代换),
∴CD∥AB(同位角相等,两直线平行).
点评 本题主要考查了平行线的性质和判定,两条直线被第三条所截,如果同位角相等,那么这两条直线平行.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
12.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:

(1)根据上面多面体的模型及表格中的数据:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)一个多面体每个顶点处都有3条棱,多面体的棱数比顶点数大10,则这个多面体的面数是12;
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱36条.若该多面体外表面三角形的个数比八边形的个数的2倍多2,求该多面体外表面三角形的个数.

(1)根据上面多面体的模型及表格中的数据:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
(2)一个多面体每个顶点处都有3条棱,多面体的棱数比顶点数大10,则这个多面体的面数是12;
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱36条.若该多面体外表面三角形的个数比八边形的个数的2倍多2,求该多面体外表面三角形的个数.
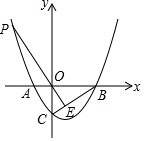 如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,点P为第二象限的抛物线上一点,且线PO交BC于E.
如图,抛物线y=x2-x-2与x轴交于A,B两点,与y轴交于C点,点P为第二象限的抛物线上一点,且线PO交BC于E.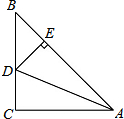 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是6,则AB,AC的长.
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是6,则AB,AC的长. 实数a,b在数轴上的位置如图所示,且|a|>|b|,化简:$\sqrt{{a}^{2}}$-$\sqrt{(a+b)^{2}}$=b.
实数a,b在数轴上的位置如图所示,且|a|>|b|,化简:$\sqrt{{a}^{2}}$-$\sqrt{(a+b)^{2}}$=b.