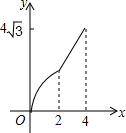题目内容
13.按要求解答下列各题:(1)解不等式组,并把解集表示在数轴上$\left\{\begin{array}{l}{1+2x>-3+x}\\{5x≤4x-1}\end{array}\right.$;
(2)解分式方程:$\frac{2-x}{x-3}$+$\frac{1}{3-x}$=1;
(3)分解因式:x2y-5xy+6y;
(4)先化简,再求值:($\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{x+2}{{x}^{2}-2x+1}$,其中x是满足-2≤x≤1的整数.
分析 (1)分别求出各不等式的解集,再在数轴上表示出来即可;
(2)先把分式方程化为整式方程求出x的值,再代入最减公分母进行检验即可;
(3)利用十字相乘法进行因式分解;
(4)先通分、化除法为乘法进行分式化简,取整数值即可.
解答 解:(1)$\left\{\begin{array}{l}{1+2x>-3+x(i)}\\{5x≤4x-1(ii)}\end{array}\right.$;
解不等式(i),得
x>-4.
解不等式(ii),得
x≤-1,
则原不等式组的解集为:-4<x≤-1.
表示在数轴上为: ;
;
(2)由原方程,得
2-x-1=x-3,
解得x=2.
经检验x=2是原方程的解,
所以x=2;
(3)x2y-5xy+6y=(xy-2y)(x-3);
(4)($\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{x+2}{{x}^{2}-2x+1}$,
=$\frac{(3x+4)-2(x+1)}{(x+1)(x-1)}$×$\frac{(x+1)^{2}}{x+2}$,
=$\frac{x+2}{(x-1)(x+1)}$×$\frac{(x+1)^{2}}{x+2}$,
=$\frac{x+1}{x-1}$.
∵x是满足-2≤x≤1的整数,x-1≠0,
∴x=-2,-1,0,
当x=-2时,原式=$\frac{-2+1}{-2-1}$=$\frac{1}{3}$;
当x=-1时,原式=$\frac{-1+1}{-1-1}$=0;
当x=0时,原式=$\frac{1}{-1}$=-1.
点评 本题综合考查了是分式的化简求值,因式分解,解一元一次不等式等,在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| 年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
| 人 数 | 1 | 4 | 3 | 2 | 2 |
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.
| A. | x>1 | B. | x≥1 | C. | x<1 | D. | x≤1 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
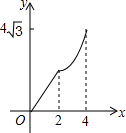
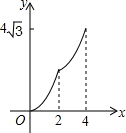
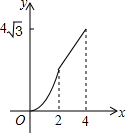
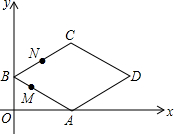 在平面直角坐标系中,四边形ABCD是菱形,其中点B的坐标是(0,2),点D的坐标是($4\sqrt{3}$,2),点M和点N是两个动点,其中点M从点B出发沿BA以每秒1个单位的速度做匀速运动,到点A后停止,同时点N从B点出发沿折线BC→CD以每秒2个单位的速度做匀速运动,如果其中一点停止运动,则另一点也停止运动.设M、N两点的运动时间为x,△BMN的面积是y,下列图象中能表示y与x的函数关系的图象大致是( )
在平面直角坐标系中,四边形ABCD是菱形,其中点B的坐标是(0,2),点D的坐标是($4\sqrt{3}$,2),点M和点N是两个动点,其中点M从点B出发沿BA以每秒1个单位的速度做匀速运动,到点A后停止,同时点N从B点出发沿折线BC→CD以每秒2个单位的速度做匀速运动,如果其中一点停止运动,则另一点也停止运动.设M、N两点的运动时间为x,△BMN的面积是y,下列图象中能表示y与x的函数关系的图象大致是( )