题目内容
18.4个数a,b,c,d排列成$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$,我们称之为二阶行列式,规定它的运算法则为:$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.若$|\begin{array}{l}{2x}&{x+1}\\{x-2}&{x+1}\end{array}|$=6,则x=-4或1.分析 根据新定义得到2x(x+1)-(x+1)(x-2)=6,然后把方程整理为一般式后利用因式分解法解方程.
解答 解:根据题意得2x(x+1)-(x+1)(x-2)=6,
整理得x2+3x-4=0,
(x+4)(x-1)=0,
x+4=0或x-1=0,
所以x1=-4,x2=1,
即x的值为-4或1.
故答案为-4或1.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
相关题目
6.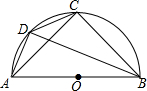 如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,D是$\widehat{AC}$上一点,且BD-AD=$\sqrt{2}$,则弦CD的长为( )
如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,D是$\widehat{AC}$上一点,且BD-AD=$\sqrt{2}$,则弦CD的长为( )
 如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,D是$\widehat{AC}$上一点,且BD-AD=$\sqrt{2}$,则弦CD的长为( )
如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,D是$\widehat{AC}$上一点,且BD-AD=$\sqrt{2}$,则弦CD的长为( )| A. | $\sqrt{2}$ | B. | $\frac{1}{2}\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
 如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=36°,则∠ABF=54°.
如图,将正方形纸片ABCD沿BE翻折,使点C落在点F处,若∠DEF=36°,则∠ABF=54°.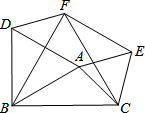 如图,在△ABC中,AB=2,AC=$\sqrt{2}$,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为2.
如图,在△ABC中,AB=2,AC=$\sqrt{2}$,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为2.