题目内容
11.如图,正方形OABC在平面直角坐标系xOy中,过点C作直线y=kx+4(k<0)交折线OAB于点D,以线段CD为边作正方形CDEF,且点E在第一象限.(1)填空:点C的坐标是(0,4);线段AB的长是4;
(2)当点D在线段OA上时,连接AE,试探究∠OAE的度数是否发生变化?若不变,求出∠OAE的度数;若有变化,请说明理由.
(3)若设点E的纵坐标为b,求出b与k的函数关系,并写出k的取值范围.
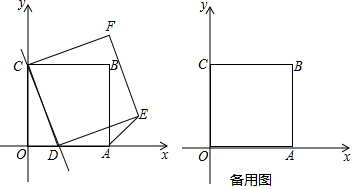
分析 (1)由直线解析式可求得C点坐标,由正方形的性质可求得AB的长;
(2)在OC上取点G,使GC=DA,可证得△CGD≌△DAE,则可求得∠OAE=∠CGD=135°;
(3)过E作EH⊥x轴于点H,可证得△OCD≌△HDE,可求得OD=EH,即可表示出D点坐标,代入直线解析式可求得b与k的关系,当点D到达A点时可知b有最大值4,则可求得k的取值范围.
解答 解:
(1)在y=kx+4中,令x=0可得y=4,
∴C(0,4),
∴OC=4,
∵四边形OABC为正方形,
∴AB=OC=4,
故答案为:(0,4);4;
(2)在OC上取点G,使GC=DA,如图1,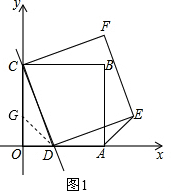
∵四边形CDEF为正方形,
∴CD=DE,∠CDE=90°,
∴∠GCD+∠CDO=∠CDO+∠EDA=90°,
∴∠GCD=∠ADE,
在△CGD和△DAE中
$\left\{\begin{array}{l}{CG=DA}\\{∠GCD=∠ADE}\\{CD=DE}\end{array}\right.$
∴△CGD≌△DAE(SAS),
∴∠CGD=∠OAE,
∵CO=OA,CG=DA,
∴OG=OD,
∴∠OGD=45°,
∴∠DGC=135°,
∴∠OAE=135°,
即∠OAE的度数不发生变化,大小为135°;
(3)过E作EH⊥x轴于点H,如图2,
由(2)可得∠OCD=∠HDE,
在△OCD和△HDE中
$\left\{\begin{array}{l}{∠OCD=∠HDE}\\{∠COD=∠DHE}\\{OC=OA}\end{array}\right.$
∴△OCD≌△HDE(AAS),
∴OD=EH=b,
∴D(b,0),
∴0=kb+4,
∴b=-$\frac{4}{k}$,
∴当k<0时,b随k的增大而增大,
当点D与A重合时,b有最大值4,代入可得4=-$\frac{4}{k}$,解得k=-1,即k的最大值为-1,
∴b与k的函数关系式为b=-$\frac{4}{k}$(k<-1).
点评 本题为一次函数的综合应用,涉及函数图象与坐标轴的交点、正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识.在(1)中确定出C点坐标是解题的关键,在(2)中构造三角形全等是解题的关键,在(3)中求得D点坐标是解题的关键.本题考查知识点较多,综合性较强,难度适中.

 已知A、B两地相距80km,甲、乙两人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DE、OC分别表示甲、乙两人离开A地的距离(km)与乙出发的时间(h)的关系,根据图象填空:
已知A、B两地相距80km,甲、乙两人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DE、OC分别表示甲、乙两人离开A地的距离(km)与乙出发的时间(h)的关系,根据图象填空: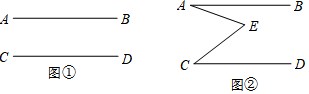
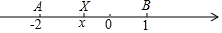 我们知道一个数x的绝对值的几何意义是:在数轴上表示这个数x的点离原点(表示数0)的距离,x的绝对值表示为|x|,也可以写成|x-0|,比如|2|=|2-0|=2;
我们知道一个数x的绝对值的几何意义是:在数轴上表示这个数x的点离原点(表示数0)的距离,x的绝对值表示为|x|,也可以写成|x-0|,比如|2|=|2-0|=2; 如图,已知:AD=BC,BE⊥AC,DF⊥AC,且BE=DF.求证:
如图,已知:AD=BC,BE⊥AC,DF⊥AC,且BE=DF.求证: