题目内容
10.观察下列等式:①1-$\frac{1}{2}$=$\frac{1}{1×2}$②$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{2×3}$③$\frac{1}{3}$-$\frac{1}{4}$=$\frac{1}{3×4}$④$\frac{1}{4}$-$\frac{1}{5}$=$\frac{1}{4×5}$;…
(1)猜想并写出第n个算式:$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n(n+1)}$
(2)我们规定:分子是1,分母是正整数的分数叫做单位分数,任意一个真分数都可以表示成不同的单位分数的和的形式,且有无数多种表示方法,根据上面的结论,请将真分数$\frac{1}{7}$表示成不同的单位分数的和的形式(写出一种即可)
分析 (1)根据给定等式的变化找出变化规律“第n个算式为:$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n(n+1)}$.”,此题得解.
(2)将$\frac{1}{7}$写成$\frac{1}{14}$+$\frac{1}{21}$+$\frac{1}{42}$即可.
解答 解:(1)观察,发现规律:①1-$\frac{1}{2}$=$\frac{1}{1×2}$,②$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{2×3}$,③$\frac{1}{3}$-$\frac{1}{4}$=$\frac{1}{3×4}$,④$\frac{1}{4}$-$\frac{1}{5}$=$\frac{1}{4×5}$,…,
∴第n个算式为:$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n(n+1)}$.
故答案为:$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n(n+1)}$.
(2)$\frac{1}{7}$=$\frac{1}{14}$+$\frac{1}{21}$+$\frac{1}{42}$.
点评 本题考查了规律型中数字的变化类,根据等式中数的变化找出变化规律是解题的关键.

练习册系列答案
相关题目
1.若直线y=kx+b经过A(0,2)和B(3,0)两点,那么这个一次函数关系式是( )
| A. | y=2x+3 | B. | y=3x+2 | C. | y=-$\frac{2}{3}$x+2 | D. | y=x-1 |
18.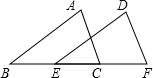 如图,BE=CF,AB=DE,添加下列哪个条件可以使△ABC≌△DEF( )
如图,BE=CF,AB=DE,添加下列哪个条件可以使△ABC≌△DEF( )
 如图,BE=CF,AB=DE,添加下列哪个条件可以使△ABC≌△DEF( )
如图,BE=CF,AB=DE,添加下列哪个条件可以使△ABC≌△DEF( )| A. | AC=DF | B. | ∠A=∠D | C. | AC∥DF | D. | BC=EF |
20.已知整数a1,a2,a3,a4…满足下列条件:a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,…,依此类推,则a2016的值为( )
| A. | -1007 | B. | -1008 | C. | -1009 | D. | -2016 |
