题目内容
3. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=2,则AB=( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=2,则AB=( )| A. | 4 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 设BC=x,根据含30度角的直角三角形性质求出AB=2BC=2x,根据勾股定理得出方程22+x2=(2x)2,求出x即可.
解答 解:设BC=x,
∵在Rt△ABC中,∠C=90°,∠A=30°,
∴AB=2BC=2x,
∵AC=2,
∴由勾股定理得:AC2+BC2=AB2,
22+x2=(2x)2,
解得:x=$\frac{2\sqrt{3}}{3}$,
∴AB=2x=$\frac{4\sqrt{3}}{3}$,
故选C.
点评 本题考查了勾股定理,含30度角的直角三角形性质的应用,解此题的关键是能得出AB=2BC,用了方程思想.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
13.下列关于x的方程中,一定是一元二次方程的为( )
| A. | ax2+bx+c=0 | B. | x2-2=(x+3)2 | C. | 2x+3x-5=0 | D. | x2-1=0 |
14.若M=2x2-12x+15,N=x2-8x+11,则M与N的大小关系为( )
| A. | M≥N | B. | M>N | C. | M≤N | D. | M<N |
15.若点(5,2)在一次函数y=kx-3(k≠0)的图象上,则k的值是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 1 |
12.在分式$\frac{b}{a+2b}$中,如果a、b都扩大为原来的3倍,则分式的值将( )
| A. | 扩大3倍 | B. | 不变 | C. | 缩小3倍 | D. | 缩小6倍 |
 如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作平行四边形ABDE,连接AD、EC.若BD=CD,求证:四边形ADCE是矩形.
如图,在△ABC中,AB=AC,D为边BC上一点,以AB、BD为邻边作平行四边形ABDE,连接AD、EC.若BD=CD,求证:四边形ADCE是矩形.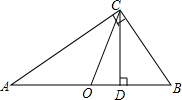 如图,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=$\sqrt{6}$,DC=$\sqrt{5}$,则△ABC的面积是$\sqrt{30}$.
如图,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=$\sqrt{6}$,DC=$\sqrt{5}$,则△ABC的面积是$\sqrt{30}$.