题目内容
18.下列变形正确的是( )| A. | 4x-5=3x+2变形得 4x-3x=2-5 | B. | $\frac{2}{3}x=\frac{3}{2}$变形得x=1 | ||
| C. | 3(x-1)=2(x+3)变形得3x-1=2x+6 | D. | $\frac{x-1}{2}-\frac{x}{5}=1$变形得3x=15 |
分析 利用去括号,移项,合并同类项,不等式的性质对四个选项逐一分析,即可得出答案.
解答 解:对于选项A,4x-5=3x+2变形得 4x-3x=2+5,
-5从左边移项到右边要变号,而选项A没变号,
∴选项A错误,故选项A不符合题意;
对于选项B,方程两边同时乘以$\frac{3}{2}$,而选项B方程左边乘以$\frac{3}{2}$,右边乘以$\frac{2}{3}$,
不满足不等式的性质2,
∴选项B错误,故选项B不符合题意;
对于选项C,去括号得,3(x-1)=2(x+3)变形得,3x-3=2x+6,
而去括号时,左边的-1没乘以3,
∴选项C错误,故选项C不符合题意;
对于选项D,去分母得,5(x-1)-2x=10,去括号得,5x-5-2x=10,
移项得,5x-2x=10+5,合并同类项得,3x=15,
∴选项D正确,符合题意.
故选:D.
点评 此题主要考查了解一元一次方程,涉及到不等式的性质,去括号,移项,合并同类项,解本题的关键不等式的性质,去括号,移项,合并同类项法则.

练习册系列答案
相关题目
6.已知a,b,c是△ABC的三条边的边长,且p=$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$,则( )
| A. | 存在三角形使得p=1或p=2 | B. | 0<p<1 | ||
| C. | 1<p<2 | D. | 2<p<3 |
13.一块砖的质量为m,体积为V,分成大小不等的两块,质量分别为m1,m2(m1>m2),体积分别为V1,V2,则( )
| A. | $\frac{m}{V}$=$\frac{{m}_{1}}{{V}_{1}}$=$\frac{{m}_{2}}{{V}_{2}}$ | B. | $\frac{m}{V}$>$\frac{{m}_{1}}{{V}_{1}}$>$\frac{{m}_{2}}{{V}_{2}}$ | ||
| C. | $\frac{{m}_{1}}{{V}_{1}}$=$\frac{{m}_{2}}{{V}_{2}}$≤$\frac{m}{V}$ | D. | $\frac{{m}_{2}}{{V}_{2}}$=$\frac{{m}_{1}}{{V}_{1}}$≥$\frac{m}{V}$ |
3.a的平方的5倍减去3的差,应写成( )
| A. | 5a2-3 | B. | 5(a2-3) | C. | (5a)2-3 | D. | a2(5-3) |
7.下列命题,真命题是( )
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 两组对角分别相等的四边形是平行四边形 | |
| D. | 在同一个圆中,相等的弦所对的弧相等 |
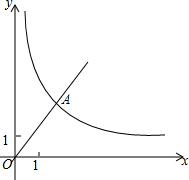 已知,如图,在平面直角坐标系xOy中,正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求:
已知,如图,在平面直角坐标系xOy中,正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求: