题目内容
6.已知a,b,c是△ABC的三条边的边长,且p=$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$,则( )| A. | 存在三角形使得p=1或p=2 | B. | 0<p<1 | ||
| C. | 1<p<2 | D. | 2<p<3 |
分析 由于分式的分子和分母都是正数,利用放大分母使分式的值变小和缩小分母使分式的值变大来确定p的范围.
解答 解:设△ABC的周长为l,
∴l=a+b+c,
∴a+b=l-c,b+c=l-a,c+a=l-c,
∵a,b,c是△ABC的三条边的边长,
∴a+b>c,b+c>a,c+a>b,
∴c<l-c<l,a<l-a<l,b<l-b<l,
∴$\frac{1}{l-c}>\frac{1}{l}$,$\frac{1}{l-a}<\frac{1}{l}$,$\frac{1}{l-b}<\frac{1}{l}$,
∴$\frac{c}{l-c}<\frac{c}{l},\frac{a}{l-a}<\frac{a}{l},\frac{b}{l-b}<\frac{b}{l}$,
∴p=$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$=$\frac{a}{l-a}+\frac{b}{l-b}+\frac{c}{l-c}$>$\frac{a}{l}+\frac{b}{l}+\frac{c}{l}$=$\frac{a+b+c}{l}$=1,
∴p>1;
设c是△ABC的三条边中的最大边,
∴c>a,c>b,
∴l-a>l-c,l-b>l-c
,∴$\frac{1}{l-a}<\frac{1}{l-c},\frac{1}{l-b}<\frac{1}{l-b}$,
∴$\frac{a}{l-a}<\frac{a}{l-c},\frac{b}{l-b}<\frac{a}{l-c}$
∴p=$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$=$\frac{a}{l-a}+\frac{b}{l-b}+\frac{c}{l-c}$<$\frac{a}{l-c}+\frac{b}{l-c}+\frac{c}{l-c}$=$\frac{a+b+c}{l-c}$=$\frac{a+b+c}{a+b}$=1+$\frac{c}{a+b}$<2,
∴p<2,
即:1<p<2.
故选C.
点评 此题是三角形的边角关系的题目,主要考查了三角形的三边关系,利用放缩法来确定p的范围是解本题的关键,也是难点.

| A. | 4x-5=3x+2变形得 4x-3x=2-5 | B. | $\frac{2}{3}x=\frac{3}{2}$变形得x=1 | ||
| C. | 3(x-1)=2(x+3)变形得3x-1=2x+6 | D. | $\frac{x-1}{2}-\frac{x}{5}=1$变形得3x=15 |
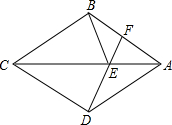 如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE.
如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE.

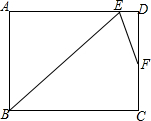 在矩形ABCD中,∠ABC的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F.若AB=9,F是CD的三等分点,则BC=6$\sqrt{2}$+3或3$\sqrt{2}$+6.
在矩形ABCD中,∠ABC的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F.若AB=9,F是CD的三等分点,则BC=6$\sqrt{2}$+3或3$\sqrt{2}$+6. 如图,在直角坐标系中,点A,点B的坐标分别为(2,0),(0,2)
如图,在直角坐标系中,点A,点B的坐标分别为(2,0),(0,2)