题目内容
10.某校八年级同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案: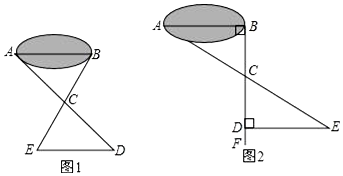
(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后回答下列问题:
(1)方案(Ⅰ)是否可行?若可行,请证明;
(2)方案(Ⅱ)是否可行?若可行,请证明;
(3)方案(Ⅱ)中若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)是否成立?否.(填是或否,不用证明)
分析 (1)由题意可证明△ACB≌△DCE,AB=DE,故方案(Ⅰ)可行;
(2)由题意可证明△ABC≌△EDC,AB=ED,故方案(Ⅱ)可行;
(3)若仅满足∠ABD=∠BDE≠90°,故此时方案(Ⅱ)不成立.
解答 解:(1)方案(Ⅰ)可行;理由如下:
∵DC=AC,EC=BC,
在△ACB和△DCE中,$\left\{\begin{array}{l}{AD=DC}\\{∠ACB=∠DCE}\\{BC=EC}\end{array}\right.$,
∴△ACB≌△DCE(SAS),
∴AB=DE,
∴测出DE的距离即为AB的长,
故方案(Ⅰ)可行.
(2)方案(Ⅱ)可行;理由如下:
∵AB⊥BC,DE⊥CD
∴∠ABC=∠EDC=90°,
在△ACB和△EDC中,$\left\{\begin{array}{l}{∠ABC=∠EDC=90°}\\{BC=DC}\\{∠ACB=∠ECD}\end{array}\right.$,
∴△ABC≌△EDC(ASA),
∴AB=ED,
∴测出DE的长即为AB的距离,
故方案(Ⅱ)可行.
(3)若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)不成立;
理由如下:若∠ABD=∠BDE≠90°,∠ACB=∠ECD,
∴△ABC∽△EDC,
∴$\frac{AB}{ED}=\frac{BC}{CD}$,
∴只要测出ED、BC、CD的长,即可求得AB的长.
但是此题没有其他条件,可能无法测出其他线段长度,
∴方案(Ⅱ)不成立;
故答案为:否.
点评 本题是三角形综合题,主要考查了全等三角形的判定与性质、相似三角形的判定和性质;本题综合性强,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
18.下列变形正确的是( )
| A. | 4x-5=3x+2变形得 4x-3x=2-5 | B. | $\frac{2}{3}x=\frac{3}{2}$变形得x=1 | ||
| C. | 3(x-1)=2(x+3)变形得3x-1=2x+6 | D. | $\frac{x-1}{2}-\frac{x}{5}=1$变形得3x=15 |
5.已知在Rt△ABC中,AD是斜边上的高,BC=3AC,那么△ABD的面积与△CBA的面积的比是( )
| A. | 1:3 | B. | 3:9 | C. | 8:1 | D. | 8:9 |
 如图所示,∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图所示,∠A+∠B+∠C+∠D+∠E+∠F=360°.
 如图,在直角坐标系中,点A,点B的坐标分别为(2,0),(0,2)
如图,在直角坐标系中,点A,点B的坐标分别为(2,0),(0,2)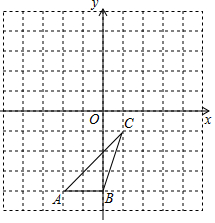 如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).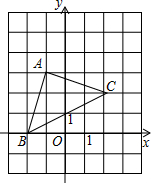 已知:如图,A(-1,3),B(-2,0),C(2,2),求△ABC的面积.
已知:如图,A(-1,3),B(-2,0),C(2,2),求△ABC的面积.