题目内容
9.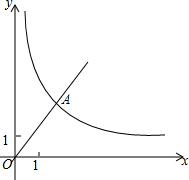 已知,如图,在平面直角坐标系xOy中,正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求:
已知,如图,在平面直角坐标系xOy中,正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求:(1)这个反比例函数的解析式;
(2)直线AB(一次函数)的表达式.
分析 (1)根据正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为4,求出点A的坐标,根据反比例函数y=$\frac{m}{x}$的图象经过点A,求出m的值即可;
(2)根据点A的坐标和等腰三角形的性质求出点B的坐标,运用待定系数法求出直线AB的表达式.
解答 解:(1)∵正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,
∴6=$\frac{3}{2}$x,
解得:x=4,
∴点A的坐标为(4,6),
∵反比例函数y=$\frac{m}{x}$的图象经过点A,
∴m=6×4=24,
∴反比例函数的解析式为:y=$\frac{24}{x}$;
(2)如图,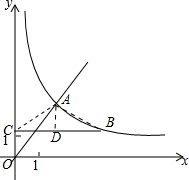 连接AC、AB,作AD⊥BC于D,
连接AC、AB,作AD⊥BC于D,
∵AC=AB,AD⊥BC,
∴BC=2CD=8,
∴点B的坐标为:(8,3),
设直线AB的表达式为:y=kx+b,
由题意得,$\left\{\begin{array}{l}{4k+b=6}\\{8k+b=3}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=9}\end{array}\right.$,
∴直线AB的表达式为:y=-$\frac{3}{4}$x+9.
点评 本题主要考查了待定系数法求反比例函数与一次函数的解析式和一次函数与反比例函数的交点的求法,注意数形结合的思想在解题中的应用.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
18.下列变形正确的是( )
| A. | 4x-5=3x+2变形得 4x-3x=2-5 | B. | $\frac{2}{3}x=\frac{3}{2}$变形得x=1 | ||
| C. | 3(x-1)=2(x+3)变形得3x-1=2x+6 | D. | $\frac{x-1}{2}-\frac{x}{5}=1$变形得3x=15 |
 如图所示,∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图所示,∠A+∠B+∠C+∠D+∠E+∠F=360°.

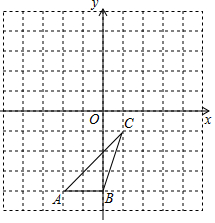 如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).