题目内容
18. 已知在平面直角坐标系中有三点A(1,2)、B(4,3)、C(3,1),请回答如下问题:
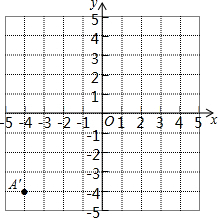
已知在平面直角坐标系中有三点A(1,2)、B(4,3)、C(3,1),请回答如下问题:(1)在平面直角坐标系内描出点A、B、C的位置,并画出三角形ABC;
(2)如图,点A′的坐标是(-4,-4),现将三角形ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点,请画出三角形A′B′C(不写画法),并求出三角形A′B′C′的面积;
(3)若M(a,b)是三角形ABC内部任意一点,请直接写出这点在三角形A′B′C′内部的对应点M′的坐标.
分析 (1)根据网格结构以及三个点的坐标,描出点A、B、C的位置,再顺次连结即可画出三角形ABC;
(2)由点A与A'的坐标,得出平移规律,根据平移规律找到B、C的对应点B′、C′的位置,再顺次连结可画出三角形A′B′C;三角形A′B′C′的面积
等于矩形的面积减去四周三角形的面积;
(3)根据(2)中图形平移的规律即可写出点M'的坐标.
解答 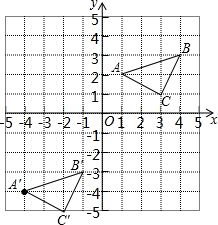 解:(1)三角形ABC如图所示;
解:(1)三角形ABC如图所示;
(2)三角形A′B′C′如图所示.
三角形A′B′C′的面积=2×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×2=$\frac{5}{2}$;
(3)∵A(1,2),A′(-4,-4),
∴△ABC向左平移5个单位,再向下平移6个单位即可得到△A′B′C′,
∴M的坐标是(a,b),
∴点M对应点M′的坐标是(a-5,b-6).
点评 本题考查的是作图-平移变换,三角形的面积,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列各式计算正确的是( )
| A. | 2a+2=3a2 | B. | (-b2)2=-b4 | C. | a2•a3=a5 | D. | (m-n)2=m2-n2 |
6.随着我国人口增长速度的减慢,小学入学儿童数量有所减少,表中的数据近似地呈现了某地区入学儿童的变化趋势.
(1)上表中年份是自变量,入学儿童人数是因变量.
(2)你预计该地区从2011年起入学儿童的人数在1600人左右.
| 年份(x) | 2006 | 2007 | 2008 | … |
| 入学儿童人数(y) | 2520 | 2330 | 2140 | … |
(2)你预计该地区从2011年起入学儿童的人数在1600人左右.
13.2的立方根是( )
| A. | $\sqrt{2}$ | B. | ±$\sqrt{2}$ | C. | $\root{3}{2}$ | D. | -$\root{3}{2}$ |