题目内容
3.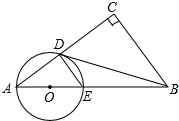 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,连接DE、DB,若∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,连接DE、DB,若∠CBD=∠A.(1)直接写出图中所有相似三角形;
(2)若AD:AO=8:5,BC=12,求⊙O的直径.
分析 (1)利用“两角法”找得图中的相似三角形即可;
(2)求出AD:AE:DE=8:10:6,根据△ADE∽△ACB,推出AD:AE:DE=AC:AB:CB=8:10:6.由此求得AC、AB的长度,然后由锐角三角函数的定义来求AE的长度.
解答 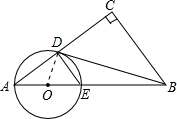 解:(1)△DBE∽△ABD,ADE∽△ACB,△BDC∽△ABC,△BDC∽△AED.
解:(1)△DBE∽△ABD,ADE∽△ACB,△BDC∽△ABC,△BDC∽△AED.
理由如下:连结OD,如图,
∵OA=OD,
∴∠A=∠ADO,
∵∠C=90°,
∴∠CBD+∠CDB=90°,
又∵∠CBD=∠A,
∴∠ADO+∠CDB=90°,
∴∠ODB=90°,
∴OD⊥DB,
∴直线BD与⊙O相切,
①由切线的性质得到:∠BDE=∠A.
又∠DBE=∠ABD,
∴△DBE∽△ABD.
②∵AE是直径,
∴∠ADE=90°.
又∠ACB=90°,
∴DE∥BC,
∴△ADE∽△ACB.
③∵∠DCB=∠BCA,∠CBD=∠A,
∴△BDC∽△ABC.
④再由相似的传递性得出:△BDC∽△AED
(2)∵AD:AO=8:5,
∴AD:AE=8:10,
∴AD:AE:DE=8:10:6.
∵△ADE∽△ACB,
∴AD:AE:DE=AC:AB:CB=8:10:6,
∵BC=12,
∴AC=16,AB=20,
∵∠CBD=∠A
∴tan∠CBD=$\frac{CD}{BC}$=$\frac{3}{4}$,则CD=9.
∴AD=AC-AD=16-9=7,
∴AE=$\frac{AD}{sinA}$=$\frac{35}{4}$.
即⊙O的直径为$\frac{35}{4}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了相似三角形的判定与性质和勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标是(8,0),tan∠ABC=$\frac{1}{2}$,△ABC的面积为8.
如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标是(8,0),tan∠ABC=$\frac{1}{2}$,△ABC的面积为8.
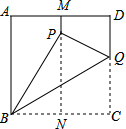 如图,有一张面积为3的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=1.
如图,有一张面积为3的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=1.