题目内容
已知tanα=3,求
的值.
| 3sinα-2cosα |
| 2cosα-sinα |
考点:同角三角函数的关系
专题:
分析:利用tanα=3,得出
=3,则sinα=3cosα,进而代入原式求出即可.
| sinα |
| cosα |
解答:解:∵tanα=3,
∴
=3,
即sinα=3cosα,
∴
=
=-1.
∴
| sinα |
| cosα |
即sinα=3cosα,
∴
| 3sinα-2cosα |
| 2cosα-sinα |
| 3cosα-2cosα |
| 2cosα-3cosα |
点评:此题主要考查了同角三角函数的关系,得出sinα=3cosα是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
今天数学课上,老师讲了多项式的加减,放学后,小明回到家拿出课堂笔记,认真的复习老师课上讲的内容,他突然发现一道题:(-x2+3xy-
y2)-(-
x2 +y2)=-
+y2)=-
x2+4xy-
y2,阴影的地方被钢笔水弄污了,那么空格中的一项是( )
| 1 |
| 2 |
| 1 |
| 2 |
 +y2)=-
+y2)=-| 1 |
| 2 |
| 3 |
| 2 |
| A、-7xy | B、+7xy |
| C、-xy | D、+xy |
下面各组线段中,能组成三角形的是( )
| A、5,11,6 |
| B、8,8,16 |
| C、10,5,6 |
| D、4,9,14 |
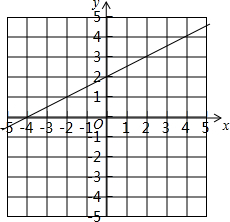 一次函数y=
一次函数y=| 1 |
| 2 |
①点(-2,1)在直线y=
| 1 |
| 2 |
②方程
| 1 |
| 2 |
③当x>0时,y>2.
④原点到直线y=
| 1 |
| 2 |
| 4 |
| 5 |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
一个两位数,个位上的数是a,十位上的数b,交换个位与十位上的数字得到一个新的两位数,则这两个两位数的和是( )
| A、a+b |
| B、2(a+b) |
| C、11(a+b) |
| D、a+10b |
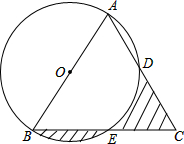 如图,在△ABC中,AB=AC=5,BC=6,以AB为直径的圆交AC于D,交BC于E,求图中阴影部分的面积.
如图,在△ABC中,AB=AC=5,BC=6,以AB为直径的圆交AC于D,交BC于E,求图中阴影部分的面积.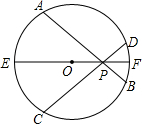 如图,在⊙O中,
如图,在⊙O中,
 如图,一个油管的横截面,其中油管的半径是5cm,有油的部分油面宽AB为8cm,则截面上有油部分油面高CD为
如图,一个油管的横截面,其中油管的半径是5cm,有油的部分油面宽AB为8cm,则截面上有油部分油面高CD为