题目内容
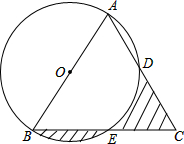 如图,在△ABC中,AB=AC=5,BC=6,以AB为直径的圆交AC于D,交BC于E,求图中阴影部分的面积.
如图,在△ABC中,AB=AC=5,BC=6,以AB为直径的圆交AC于D,交BC于E,求图中阴影部分的面积.考点:扇形面积的计算
专题:
分析:首选利用已知得出
=
,即阴影部分面积之和即为S△DEC,进而利用相似三角形的判定与性质求出即可.
 |
| BE |
 |
| DE |
解答: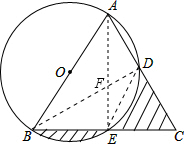 解:连接AE、BD、DE,
解:连接AE、BD、DE,
∵∠AEB=90°,AB=AC,
∴∠BAE=∠CAE,BE=CE(三线合一)
∵∠EBD=∠EAD(同弧所对的圆周角相等),
∴∠BAE=∠DBE,
∴
=
,
即阴影部分面积之和即为S△DEC,
∵DE=EC(直角三角形斜边上的中线等于斜边的一半),
∴∠C=∠EDC
∴△DEC∽△ABC,
∴相似比=EC:AB=3:5,
S△DEC:S△ABC=9:25,S△ABC=12,
∴阴影部分面积为:S△DEC=
.
 解:连接AE、BD、DE,
解:连接AE、BD、DE,∵∠AEB=90°,AB=AC,
∴∠BAE=∠CAE,BE=CE(三线合一)
∵∠EBD=∠EAD(同弧所对的圆周角相等),
∴∠BAE=∠DBE,
∴
 |
| BE |
 |
| DE |
即阴影部分面积之和即为S△DEC,
∵DE=EC(直角三角形斜边上的中线等于斜边的一半),
∴∠C=∠EDC
∴△DEC∽△ABC,
∴相似比=EC:AB=3:5,
S△DEC:S△ABC=9:25,S△ABC=12,
∴阴影部分面积为:S△DEC=
| 108 |
| 25 |
点评:此题主要考查了相似三角形的判定与性质以及扇形面积求法,得出阴影部分面积之和即为S△DEC是解题关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,∠1=78°,且∠1:∠2=13:17,则a、b的位置关系是( )
如图,∠1=78°,且∠1:∠2=13:17,则a、b的位置关系是( )| A、相交 | B、平行 |
| C、垂直 | D、无法确定 |
 如图,在△ABC中,AB=AC,AD=DE,若∠BAD=18°,∠EDC=12°,则∠ADE=( )
如图,在△ABC中,AB=AC,AD=DE,若∠BAD=18°,∠EDC=12°,则∠ADE=( )| A、56° | B、58° |
| C、60° | D、62° |
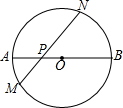 如图,在⊙O中,AB是直径,P是AB上一点,过点P作弦MN,∠NPB=45°.
如图,在⊙O中,AB是直径,P是AB上一点,过点P作弦MN,∠NPB=45°. 如图,四边ABCD是圆的内接四边形,若∠ABC=50°,则∠ADC=
如图,四边ABCD是圆的内接四边形,若∠ABC=50°,则∠ADC=