题目内容
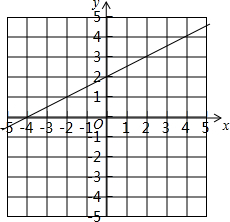 一次函数y=
一次函数y=| 1 |
| 2 |
①点(-2,1)在直线y=
| 1 |
| 2 |
②方程
| 1 |
| 2 |
③当x>0时,y>2.
④原点到直线y=
| 1 |
| 2 |
| 4 |
| 5 |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:一次函数的图象,一次函数图象上点的坐标特征,一次函数与一元一次方程
专题:
分析:①③根据函数的图象直接进行解答即可;
②根据解析式求得与x轴的交点即可判定方程
x+2=0的解;
④根据三角形相似对应边成比例即可求得原点到直线y=
x+2的距离.
②根据解析式求得与x轴的交点即可判定方程
| 1 |
| 2 |
④根据三角形相似对应边成比例即可求得原点到直线y=
| 1 |
| 2 |
解答:解:由函数y=
x+2的图象可知,点(-2,1)在直线y=
x+2上,①正确;
由函数y=
x+2与x轴的交点为(-4,0)可知方程
x+2=0的解为x=-4,故②正确;
由函数y=
x+2的图象可知,当x>0时,y>2,故③正确;
由
=
,解得d=
,故④正确.
故答案为D.
| 1 |
| 2 |
| 1 |
| 2 |
由函数y=
| 1 |
| 2 |
| 1 |
| 2 |
由函数y=
| 1 |
| 2 |
由
| d |
| 4 |
| 2 | ||
|
| 4 |
| 5 |
| 5 |
故答案为D.
点评:本题考查的是一次函数的图象,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AB=AC,AD=DE,若∠BAD=18°,∠EDC=12°,则∠ADE=( )
如图,在△ABC中,AB=AC,AD=DE,若∠BAD=18°,∠EDC=12°,则∠ADE=( )| A、56° | B、58° |
| C、60° | D、62° |
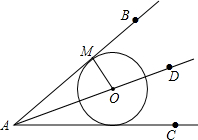 点O为∠BAC的角平分线AD上一点,以O为圆心的圆与AB相切于点M,求证:AC为⊙O的切线.
点O为∠BAC的角平分线AD上一点,以O为圆心的圆与AB相切于点M,求证:AC为⊙O的切线. 如图,在小正方形组成的网格中,图②是由图①经过旋转变换得到的,其旋转中心是点
如图,在小正方形组成的网格中,图②是由图①经过旋转变换得到的,其旋转中心是点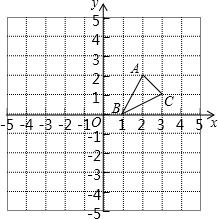 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2),B(1,0),C(3,1)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2),B(1,0),C(3,1)