题目内容
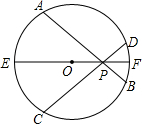 如图,在⊙O中,
如图,在⊙O中, |
| AB |
 |
| CD |
考点:圆心角、弧、弦的关系
专题:计算题
分析:作OH⊥AB于H,OG⊥CD于G,如图,根据在同圆或等圆中,相等的弦所对应的弦心距相等,由AB=CD得OH=OG,根据角平分线的判定得到OP平分∠APC,然后根据等角的补角相等即可得到∠APF=∠CPF.
解答: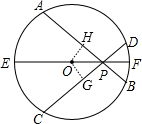 解:∠APF与∠CPF相等.理由如下:
解:∠APF与∠CPF相等.理由如下:
作OH⊥AB于H,OG⊥CD于G,如图,
∵AB=CD,
∴OH=OG,
∴OP平分∠APC,
即∠APE=∠CPE,
∴∠APF=∠CPF.
 解:∠APF与∠CPF相等.理由如下:
解:∠APF与∠CPF相等.理由如下:作OH⊥AB于H,OG⊥CD于G,如图,
∵AB=CD,
∴OH=OG,
∴OP平分∠APC,
即∠APE=∠CPE,
∴∠APF=∠CPF.
点评:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
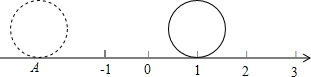 如图所示,直径为单位1的圆从数轴上表示1的点沿着数轴无滑动地逆时针滚动一周到达A点,则A点表示的数是( )
如图所示,直径为单位1的圆从数轴上表示1的点沿着数轴无滑动地逆时针滚动一周到达A点,则A点表示的数是( )| A、-π+1 | B、-π-1 |
| C、π+1 | D、π-1 |
 如图,已知点A的坐标为(-1,0),且AB=AC=
如图,已知点A的坐标为(-1,0),且AB=AC= 如图,在小正方形组成的网格中,图②是由图①经过旋转变换得到的,其旋转中心是点
如图,在小正方形组成的网格中,图②是由图①经过旋转变换得到的,其旋转中心是点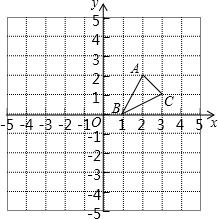 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2),B(1,0),C(3,1)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2),B(1,0),C(3,1) 如图,直线AB、CD相交于O点,若∠COE=∠FOB=90°,∠AOC=30°,则∠EOF=
如图,直线AB、CD相交于O点,若∠COE=∠FOB=90°,∠AOC=30°,则∠EOF=