题目内容
将下列各数填在相应的括号里:
-2.5,5
,0,8,-2,
,0.7,-
,-1.121121112…,
,-0.05.
正数集合{ …};
负数集合{ …};
整数集合{ …};
有理数集合{ …};
无理数集合{ …}.
-2.5,5
| 1 |
| 2 |
| π |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
正数集合{ …};
负数集合{ …};
整数集合{ …};
有理数集合{ …};
无理数集合{ …}.
考点:实数
专题:
分析:根据有理数的分类实数
进行填空即可.
|
解答:解:正数集合{ 5
,0,8,
,0.7,
,…};
负数集合{-2.5,-2,-
,-1.121121112…,-0.05 …};
整数集合{ 0,8,-2,…};
有理数集合{-2.5,5
,0,8,-2,0.7,-
,
,-0.05 …};
无理数集合{
,-1.121121112…,…}.
| 1 |
| 2 |
| π |
| 2 |
| 3 |
| 4 |
负数集合{-2.5,-2,-
| 2 |
| 3 |
整数集合{ 0,8,-2,…};
有理数集合{-2.5,5
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
无理数集合{
| π |
| 2 |
点评:本题考查了实数、无理数、有理数之间的关系,有理数都可以化为小数,其中整数可以看作小数点后面是零的小数,分数都可以化为有限小数或无限循环小数;无理数是无限不循环小数,其中有开方开不尽的数.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
如图是一个几何体的三视图,根据图纸标注的数据,求得这个几何体的侧面积是( )


| A、12π | B、15π |
| C、24π | D、30π |
 如图,已知AB∥CD,AB=CD,BF=CE,求证:AE=DF.
如图,已知AB∥CD,AB=CD,BF=CE,求证:AE=DF.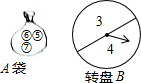 学习概率知识以后,小庆和小丽设计了一个游戏.在一个不透明的布袋A里面装有三个分别标有数字5,6,7的小球(小球除数字不同外,其余都相同);同时制作了一个可以自由转动的转盘B,转盘B被平均分成2部分,在每一部分内分别标上数字3,4.现在其中一人从布袋A中随机摸取一个小球,记下数字为x;另一人转动转盘B,转盘停止后,指针指向的数字记为y(若指针指在边界线上时视为无效,重新转动),从而确定点P的坐标为P(x,y).
学习概率知识以后,小庆和小丽设计了一个游戏.在一个不透明的布袋A里面装有三个分别标有数字5,6,7的小球(小球除数字不同外,其余都相同);同时制作了一个可以自由转动的转盘B,转盘B被平均分成2部分,在每一部分内分别标上数字3,4.现在其中一人从布袋A中随机摸取一个小球,记下数字为x;另一人转动转盘B,转盘停止后,指针指向的数字记为y(若指针指在边界线上时视为无效,重新转动),从而确定点P的坐标为P(x,y). 如图:在△ABC中,CD、BE分别是AB、AC边上的高,∠EBC=45°,∠DCB=30°,DC=12,求BE的长.
如图:在△ABC中,CD、BE分别是AB、AC边上的高,∠EBC=45°,∠DCB=30°,DC=12,求BE的长.