题目内容
如图，已知AB∥CD，AB=CD，BF=CE，求证：AE=DF．考点：全等三角形的判定与性质
专题：证明题
分析：易证∠DCF=∠ABE，CF=BE，即可证明△ABE≌△DCF，可得AE=DF，即可解题．
解答：证明：AB∥CD，
∴∠DCF=∠ABE，
∵BF=CE，
∴BF-EF=CE-EF，即CF=BE，
在△ABE与△DCF中，
，
∴△ABE≌△DCF（SAS），
∴AE=DF．
∴∠DCF=∠ABE，
∵BF=CE，
∴BF-EF=CE-EF，即CF=BE，
在△ABE与△DCF中，
|
∴△ABE≌△DCF（SAS），
∴AE=DF．
点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△ABE≌△DCF是解题的关键．
练习册系列答案
相关题目
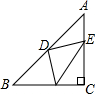已知：如图所示Rt△ABC中，∠C=90°，AC=BC，D是AB中点，E、F分别是AC、BC边上的两动点，无论E、F如何运动，始终保持AE=CF．求证：△DEF是等腰直角三角形．
如图，在△ABC中，D为BC边上的一点，若a-|a|=2a，则实数a在数轴上的对应点一定在（ ）
| A、原点左侧 |
| B、原点或原点左侧 |
| C、原点右侧 |
| D、原点或原点右侧 |
如图，矩形ABCD中，点M是CD的中点，点P是AB上的一动点，若AD=1，AB=2，则PA+PB+PM的最小值是