题目内容
12.在下列横线内填上适当的整式,使等式成立.(1)3m2n-mn2=mn(3m-n)(2)$\frac{x^2}{4}$+xy+y2=($\frac{x}{2}$+y)2
(3)$\frac{a-{a}^{2}}{ab}$=$\frac{()}{b}$1-a(4)$\frac{m}{m-n}$=-$\frac{m}{()}$n-m.
分析 (1)根据提公因式法,可分解因式;
(2)根据完全平方公式,可分解因式;
(3)根据分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变,可得答案;
(4)分子、分母、分式改变其中的任意两个的符号,分式的值不变,可得答案.
解答 解:(1)3m2n-mn2=mn (3m-n);
(2)$\frac{x^2}{4}$+xy+y2=($\frac{x}{2}$+y)2;
(3)$\frac{a-{a}^{2}}{ab}$=$\frac{()}{b}$ 1-a(4)$\frac{m}{m-n}$=-$\frac{m}{()}$ n-m.
故答案为:3m-n;($\frac{1}{2}$x+y)2,1-a;n-m.
点评 本题考查了分式的基本性质,分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变,注意分子、分母、分式改变其中的任意两个的符号,分式的值不变.

练习册系列答案
相关题目
7.在-5,-$\sqrt{3}$,-3,0这四个实数中,最大的是( )
| A. | -3 | B. | -$\sqrt{3}$ | C. | -1 | D. | 0 |
2.下列计算错误的是( )
| A. | x3m+1=(x3)m+1 | B. | x3m+1=x•x3m | C. | x3m+1=xm•x2m•x | D. | x3m+1=(xm)3•x |
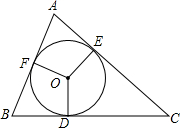 △ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,且AB=11cm,BC=16cm,CA=15cm,求AF、BD、CE的长?
△ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,且AB=11cm,BC=16cm,CA=15cm,求AF、BD、CE的长? 如图,△ABC中,∠C=90°,AC=BC,AB=a(a>0),∠CAB的平分线交BC于点D,DE⊥AB垂足为E,则△DEB的周长等于a.
如图,△ABC中,∠C=90°,AC=BC,AB=a(a>0),∠CAB的平分线交BC于点D,DE⊥AB垂足为E,则△DEB的周长等于a.