题目内容
2．
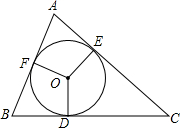△ABC的内切圆⊙O与BC，CA，AB分别相切于点D、E、F，且AB=11cm，BC=16cm，CA=15cm，求AF、BD、CE的长？
分析 由切线长定理可知；AF=AE，BF=BD，CD=CE，设AF=AE=x，则BF=BD=11-x，EC=DC=15-x，然后根据BD+DC=16列方程求解即可．
解答 解：∵△ABC的内切圆⊙O与BC，CA，AB分别相切于点D、E、F，
∴AF=AE，BF=BD，CD=CE．
设AF=AE=x，则BF=BD=11-x，EC=DC=15-x．
根据题意得11-x+15-x=16．
解得；x=5cm．
∴AF=5cm．BD=11-x=11-5=6cm，EC=15-x=10cm．
∴AF=5cm，BD=6cm，EC=10cm．
点评 本题主要考查的是切线长定理的应用，根据切线长定理列出关于x的方程是解题的关键．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
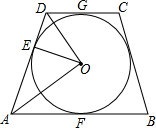在四边形ABCD中，AB∥CD，⊙O分别与AD、AB、CD相切于E、F、G，连接OA、OD、OE．求证：∠AOE=$\frac{1}{2}$∠ADC．
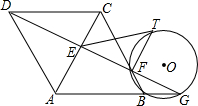已知：?ABCD过点D作直线交AC于E，交BC于F，交AB的延长线于G，经过B、G、F三点作⊙O，过E作⊙O的切线ET，T为切点．求证：ET=ED．
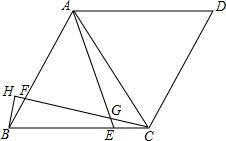已知菱形ABCD，∠D=60°，点E在BC上，点F在AB上，BF=CE，连接CF，AE交于点G，作BH⊥CF交CF延长线于H，若CG=2，则BH的长为$\sqrt{3}$．
11．下面四组代数式，是同类项的是（ ）
| A． | 2a和a2 | B． | 4b和4a | C． | -6a2b和-3ab3 | D． | -2x2和6x2 |