题目内容
17. 如图,△ABC中,∠C=90°,AC=BC,AB=a(a>0),∠CAB的平分线交BC于点D,DE⊥AB垂足为E,则△DEB的周长等于a.
如图,△ABC中,∠C=90°,AC=BC,AB=a(a>0),∠CAB的平分线交BC于点D,DE⊥AB垂足为E,则△DEB的周长等于a.
分析 先利用AAS判定△ACD≌△AED得出AC=AE,CD=DE;再对构成△DEB的几条边进行变换,可得到其周长等于AB的长.
解答 解:∵AD平分∠CAB交BC于点D,
∴∠CAD=∠EAD,
∵DE⊥AB,
∴∠AED=∠C=90,
在△ACD与△AED中,$\left\{\begin{array}{l}{∠CAD=∠EAD}\\{∠C=∠AED=90°}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△AED,
∴AC=AE,CD=DE,
∵∠C=90°,AC=BC,
∴∠B=45°,
∴DE=BE,
∵AC=BC,AB=a,
∴2BC2=AB2,即BC=$\frac{\sqrt{2}}{2}$a,
∴BE=AB-AE=AB-AC=a-$\frac{\sqrt{2}}{2}$a,
∴BC+BE=$\frac{\sqrt{2}}{2}$a+a-$\frac{\sqrt{2}}{2}$a=a
∵△DEB的周长=DE+DB+BE=BC+BE=a,
故答案为:a.
点评 本题考查了角平分线的性质,等腰直角三角形的性质,全等三角形的判定和性质,熟练掌握角平分线的性质是解题的关键.

练习册系列答案
相关题目
2. 如图,已知AB=CD,AE=CF,要证明△ABF≌△CDE,还需添加的已知条件是( )
如图,已知AB=CD,AE=CF,要证明△ABF≌△CDE,还需添加的已知条件是( )
 如图,已知AB=CD,AE=CF,要证明△ABF≌△CDE,还需添加的已知条件是( )
如图,已知AB=CD,AE=CF,要证明△ABF≌△CDE,还需添加的已知条件是( )| A. | ∠B=∠D | B. | BF∥DE | C. | BF=DE | D. | AF=CE |
9.在数轴上,与表示-5的点距离等于3的点所表示的数是( )
| A. | 2 | B. | -2 | C. | -8 | D. | -8或-2 |
6.下列各组几何图形中结论不正确的是( )
| A. | 有一边和一个锐角相等的两个直角三角形全等 | |
| B. | 斜边和一个锐角对应相等的两个直角三角形全等 | |
| C. | 两条直角边对应相等的两个直角三角形全等 | |
| D. | 斜边和直角边对应相等的两个直角三角形全等 |
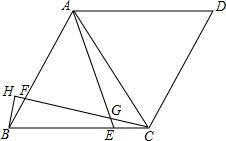 已知菱形ABCD,∠D=60°,点E在BC上,点F在AB上,BF=CE,连接CF,AE交于点G,作BH⊥CF交CF延长线于H,若CG=2,则BH的长为$\sqrt{3}$.
已知菱形ABCD,∠D=60°,点E在BC上,点F在AB上,BF=CE,连接CF,AE交于点G,作BH⊥CF交CF延长线于H,若CG=2,则BH的长为$\sqrt{3}$.