题目内容
13. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=8,求斜边AB的长.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=8,求斜边AB的长.
分析 设BC=x,则AB=2x,再根据勾股定理求出x的值,进而得出结论.
解答 解:∵在Rt△ABC中,∠C=90°,∠A=30°,AC=8,
∴设BC=x,则AB=2x,
∵AC2+BC2=AB2,即(8)2+x2=(2x)2,
解得x=$\frac{8\sqrt{3}}{3}$,
∴AB=2x=$\frac{16\sqrt{3}}{3}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
1.下面是三角形三边的比,其中是直角三角形三边的比的是( )
| A. | 2:1:2 | B. | 2:3:4 | C. | 1:1:$\sqrt{2}$ | D. | 4:5:6 |

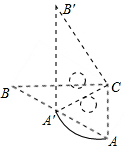 如图,△ABC和△A′B′C′是两个完全重合的直角三角板,∠B=30°,斜边长为10cm,三角板A′B′C′绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长是多少?
如图,△ABC和△A′B′C′是两个完全重合的直角三角板,∠B=30°,斜边长为10cm,三角板A′B′C′绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长是多少?