题目内容
13.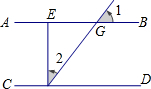 如图,若AB∥CD,EF⊥CD,∠1=54°,则∠2为( )
如图,若AB∥CD,EF⊥CD,∠1=54°,则∠2为( )| A. | 54° | B. | 46° | C. | 44° | D. | 36° |
分析 首先根据AB∥CD,可得∠1=∠3=54°,然后根据EF⊥CD,求得∠2=90°-∠3.
解答  解:∵AB∥CD,
解:∵AB∥CD,
∴∠1=∠3=54°,
∵EF⊥CD,
∴∠2=90°-∠3=90°-54°=36°.
故选D.
点评 本题考查了平行线的性质,解答本题的关键是掌握平行线的性质:两直线平行,同位角相等.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
18.若关于x的分式方程$\frac{x}{x-2}$-2m=$\frac{3m}{x-2}$无解,则m的值为( )
| A. | m=$\frac{2}{3}$ | B. | m=$\frac{2}{3}$或m=2 | C. | m=$\frac{1}{2}$ | D. | m=$\frac{2}{3}$或m=$\frac{1}{2}$ |
2.若关于x的不等式mx-n>0的解集是$x<\frac{1}{7}$,则关于x的不等式(m+n)x>n-m的解集是( )
| A. | x<-$\frac{3}{4}$ | B. | x>-$\frac{3}{4}$ | C. | x>$\frac{3}{4}$ | D. | x<$\frac{3}{4}$ |
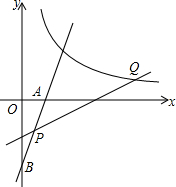 如图,直线l:y=kx-2k交坐标轴于A,B两点,点P(m,n)为直线l上的一点,且满足关系式2m2+2n2-4m+8n+10=0.
如图,直线l:y=kx-2k交坐标轴于A,B两点,点P(m,n)为直线l上的一点,且满足关系式2m2+2n2-4m+8n+10=0.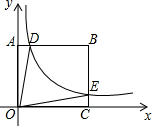 如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC上的点E,且2CE=BE,交AB于点D.若四边形ODBE的面积为8,则k=8.
如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC上的点E,且2CE=BE,交AB于点D.若四边形ODBE的面积为8,则k=8. 如图,小红用一张长方形纸片ABCD进行折纸,已知AB=8cm,BC=10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),求EC.
如图,小红用一张长方形纸片ABCD进行折纸,已知AB=8cm,BC=10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),求EC.