题目内容
12.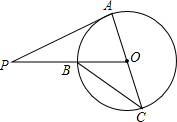 如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,PO交⊙O于点B,若∠P=20°,则∠BCA=35度.
如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,PO交⊙O于点B,若∠P=20°,则∠BCA=35度.
分析 根据PA是⊙O的切线,AC是⊙O的直径,得到∠A=90°,根据三角形的内角和得到∠AOB=70°,即可得到结果.
解答 解:∵PA是⊙O的切线,AC是⊙O的直径,
∴∠A=90°,
∵∠P=20°,
∴∠AOB=70°,
∴∠BCA=35°,
故答案为:35.
点评 本题考查了切线的性质,圆周角定理,熟练掌握切线的性质是解题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
2.若关于x的不等式mx-n>0的解集是$x<\frac{1}{7}$,则关于x的不等式(m+n)x>n-m的解集是( )
| A. | x<-$\frac{3}{4}$ | B. | x>-$\frac{3}{4}$ | C. | x>$\frac{3}{4}$ | D. | x<$\frac{3}{4}$ |
7.A市为制定居民用水价格调整方案,就每月的用水量、可承受的水价调整幅度等进行民意调查,调查采用随机抽样的方式.图1、图2为某一小区的调查数据统计图.
已知被调查居民每户每月的用水量在5m3~35m3之间,被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,试回答下列问题:
(1)请补全图1的统计图;
(2)被调查居民用水量的中位数落在什么范围内:10m3~15m3(直接填写范围即可,如5m3~35m3等);
(3)若采用阶梯式累进制调价方案(如下表所示),试估计该小区有百分之几的居民用水费用的增长幅度不超过50%?
阶梯式累进制自来水调价方案
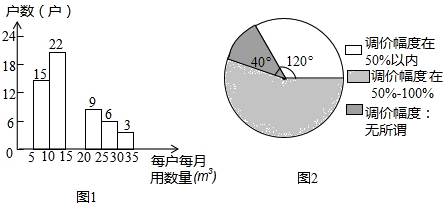
已知被调查居民每户每月的用水量在5m3~35m3之间,被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,试回答下列问题:
(1)请补全图1的统计图;
(2)被调查居民用水量的中位数落在什么范围内:10m3~15m3(直接填写范围即可,如5m3~35m3等);
(3)若采用阶梯式累进制调价方案(如下表所示),试估计该小区有百分之几的居民用水费用的增长幅度不超过50%?
阶梯式累进制自来水调价方案
| 级数 | 用水量范围 | 现行价格(元/m3) | 调整后价格(元/m3) |
| 第一级 | 0~15m3(含15m3) | 1.80 | 2.50 |
| 第二级 | 15m3以上 | 1.80 | 3.30 |

17.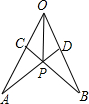 如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
 如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
1.下面是三角形三边的比,其中是直角三角形三边的比的是( )
| A. | 2:1:2 | B. | 2:3:4 | C. | 1:1:$\sqrt{2}$ | D. | 4:5:6 |
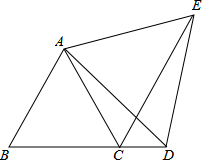 如图,△ABC为等边三角形,点D在BC的延长线上,CE平分∠ACD,且∠ADE=60°.
如图,△ABC为等边三角形,点D在BC的延长线上,CE平分∠ACD,且∠ADE=60°.