题目内容
 如图,平行四边形ABCD中,点M为BC边中点,且AM=9,BD=12,AD=10,AM与BD的交于点E.求证:AM⊥BD.
如图,平行四边形ABCD中,点M为BC边中点,且AM=9,BD=12,AD=10,AM与BD的交于点E.求证:AM⊥BD.考点:相似三角形的判定与性质,勾股定理的逆定理,平行四边形的性质
专题:证明题
分析:易证△BEM∽△DEA,根据相似三角形的对应边的比相等,即可求得BE和EM的长,然后在△BEM中,利用勾股定理的逆定理即可判断.
解答:证明:∵在?ABCD中,BC=AD=10,且M为BC边中点,
∴BM=
BC=5.
∵在?ABCD中,BC∥AD,
∴∠MBE=∠ADE,∠EMB=∠EAD,
∴△BEM∽△DEA,
∴
=
=
=
=
,
又∵AM=9,BD=12,
∴ME=3,BE=4,
∵在△BME中,ME2+BE2=32+42=25,BM2=52=25,
∴ME2+BE2=BM2,
∴BE⊥ME,即:AM⊥BD.
∴BM=
| 1 |
| 2 |
∵在?ABCD中,BC∥AD,
∴∠MBE=∠ADE,∠EMB=∠EAD,
∴△BEM∽△DEA,
∴
| ME |
| AE |
| BE |
| DE |
| BM |
| AD |
| 5 |
| 10 |
| 1 |
| 2 |
又∵AM=9,BD=12,
∴ME=3,BE=4,
∵在△BME中,ME2+BE2=32+42=25,BM2=52=25,
∴ME2+BE2=BM2,
∴BE⊥ME,即:AM⊥BD.
点评:本题考查了相似三角形的判定与性质以及勾股定理的逆定理,正确利用相似三角形的性质求得BE和EM的长是关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目

 如图,在Rt△OAB中,∠A=90°,∠ABO=30°,OB=
如图,在Rt△OAB中,∠A=90°,∠ABO=30°,OB=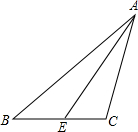 如图,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.
如图,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.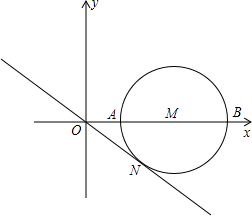 如图所示,在平面直角坐标中,M是x轴正半轴上一点,⊙M与x轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程x2-4x+3=0的两根,ON是⊙M的切线,N为切点,N在第四象限.
如图所示,在平面直角坐标中,M是x轴正半轴上一点,⊙M与x轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程x2-4x+3=0的两根,ON是⊙M的切线,N为切点,N在第四象限.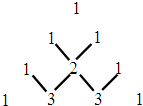 如图是我国古代数学家发现的,称为“杨辉三角形”,它的发现比西方要早五百年左右.“杨辉三角形”中有许多规律,如(a+b)2=a2+2ab+b2开式中的系数1、2、1恰好对应图中第三行的数字; (a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式.(a+b)4=
如图是我国古代数学家发现的,称为“杨辉三角形”,它的发现比西方要早五百年左右.“杨辉三角形”中有许多规律,如(a+b)2=a2+2ab+b2开式中的系数1、2、1恰好对应图中第三行的数字; (a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式.(a+b)4= 如图,已知直线CD、EF相交于点O,OA⊥OB,且OC平分∠AOF,∠BOE=2∠AOE.则∠BOD=
如图,已知直线CD、EF相交于点O,OA⊥OB,且OC平分∠AOF,∠BOE=2∠AOE.则∠BOD=