题目内容
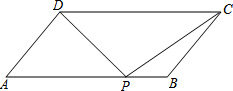 如图,平行四边形ABCD中,AB+BC=20,sinA=
如图,平行四边形ABCD中,AB+BC=20,sinA=| 4 |
| 5 |
(1)求y与x的函数关系式,并求△PCD的面积的最大值;
(2)若以DC为直径的圆过P、B两点,求AP的长.
考点:平行四边形的性质,二次函数的最值,圆周角定理,解直角三角形
专题:
分析:(1)首先作DH⊥AB于H,在平行四边形ABCD中,AB=DC=x,AD=BC=20-x,由AB+BC=20,sinA=
,可得y与x的函数关系式为:y=
×
(20-x)x,继而求得答案;
(2)首先连接BD,由sin∠BCD=sinA=
,可得BC=
CD,继而求得x的值,然后由以DC为直径的圆过P、B两点,证得∠APD=∠A,又由DH⊥AB,可求得AP=2AH=2×
×(20-
)=9.
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
(2)首先连接BD,由sin∠BCD=sinA=
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 25 |
| 2 |
解答: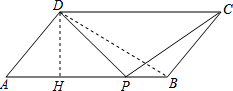 解:(1)作DH⊥AB于H,
解:(1)作DH⊥AB于H,
在平行四边形ABCD中,AB=DC=x,AD=BC=20-x,
在Rt△ADH中,DH=AD×sinA=
(20-x),
y与x的函数关系式为:y=
×
(20-x)x,
即:y=-
x2+8x,
∵y=-
x2+8x=-
(x-10)2+40,
∴当x=10时,y的最大值为40
∴△PCD的面积的最大值为40;
(2)连接BD,由题意得:∠DBC=90°
∵sin∠BCD=sinA=
,
∴cosA=
,
∴BC=
CD,
∴20-x=
x,
∴x=
,
∵D、C、B、P在同一个圆上,
∴∠BCD+∠BPD=180°,
∵∠APD+∠BPD=180°,
∴∠APD=∠BCD,
∴∠APD=∠A,
∵DH⊥AB,
∴AP=2AH=2×
×(20-
)=9.
 解:(1)作DH⊥AB于H,
解:(1)作DH⊥AB于H,在平行四边形ABCD中,AB=DC=x,AD=BC=20-x,
在Rt△ADH中,DH=AD×sinA=
| 4 |
| 5 |
y与x的函数关系式为:y=
| 1 |
| 2 |
| 4 |
| 5 |
即:y=-
| 2 |
| 5 |
∵y=-
| 2 |
| 5 |
| 2 |
| 5 |
∴当x=10时,y的最大值为40
∴△PCD的面积的最大值为40;
(2)连接BD,由题意得:∠DBC=90°
∵sin∠BCD=sinA=
| 4 |
| 5 |
∴cosA=
| 3 |
| 5 |
∴BC=
| 3 |
| 5 |
∴20-x=
| 3 |
| 5 |
∴x=
| 25 |
| 2 |
∵D、C、B、P在同一个圆上,
∴∠BCD+∠BPD=180°,
∵∠APD+∠BPD=180°,
∴∠APD=∠BCD,
∴∠APD=∠A,
∵DH⊥AB,
∴AP=2AH=2×
| 3 |
| 5 |
| 25 |
| 2 |
点评:此题考查了平行四边形的性质、二次函数的最值、三角函数以及圆的内接四边形的性质.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各数为无理数的是( )
| A、0.7256 | ||||
B、
| ||||
C、
| ||||
D、
|
 有理数a、b在数轴上的位置如图所示,则a-b的结果一定是( )
有理数a、b在数轴上的位置如图所示,则a-b的结果一定是( )| A、整数 | B、分数 | C、正数 | D、负数 |
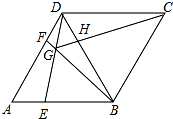 如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )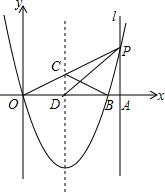 直线l垂直x轴于点A(4,0),点P是l上的一个动点,经过点P的抛物线y=x2+bx+c与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,连接PD、PB、BC,设点P的纵坐标为m.
直线l垂直x轴于点A(4,0),点P是l上的一个动点,经过点P的抛物线y=x2+bx+c与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,连接PD、PB、BC,设点P的纵坐标为m.