题目内容
11. 如图所示是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上,当∠A=30°,AC=10时,两直角顶点C,C1的距离是5.
如图所示是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上,当∠A=30°,AC=10时,两直角顶点C,C1的距离是5.
分析 连接CC1,根据M是AC、A1C1的中点,AC=A1C1,得出CM=A1M=C1M=$\frac{1}{2}$AC=5,再根据∠A1=∠A1CM=30°,得出∠CMC1=60°,△MCC1为等边三角形,从而证出CC1=CM,即可得出答案.
解答  解:如图,连接CC1,
解:如图,连接CC1,
∵两块三角板重叠在一起,较长直角边的中点为M,
∴M是AC、A1C1的中点,AC=A1C1,
∴CM=A1M=C1M=$\frac{1}{2}$AC=5,
∴∠A1=∠A1CM=30°,
∴∠CMC1=60°,
∴△CMC1为等边三角形,
∴CC1=CM=5,
∴CC1长为5.
故答案为5.
点评 本题考查了旋转的性质,等边三角形的判定与性质,证明出△MCC1为等边三角形是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
19.已知n是正整数,且$\sqrt{45n}$也是一个正整数,则正整数n的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 9 |
6.计算25m÷5m的结果为( )
| A. | 5 | B. | 5m | C. | 20 | D. | 20m |
20.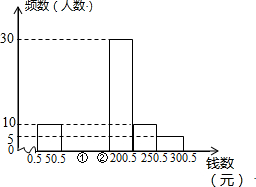 某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
(1)补全频数分布表和直方图;
(2)研究所认为,应对消费150元以上的学生提出勤俭节约的建议,试估计应对该校4000名学生中约多少名学生提出这项建议?
 某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.(1)补全频数分布表和直方图;
(2)研究所认为,应对消费150元以上的学生提出勤俭节约的建议,试估计应对该校4000名学生中约多少名学生提出这项建议?
| 分 组 | 频数 | 所占比例 |
| 0.5~50.5 | 10 | 0.1 |
| 50.5~100.5 | 20 | 0.2 |
| 100.5~150.5 | 35 | 35 |
| 150.5~200.5 | 30 | 0.3 |
| 200.5~250.5 | 10 | 0.1 |
| 250.5~300.5 | 5 | 0.05 |
| 合 计 | 100 | ------ |
1.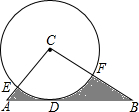 如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )| A. | $\frac{32}{3}\sqrt{3}-4π$ | B. | $\frac{32}{3}\sqrt{3}-2π$ | C. | 16-4π | D. | 16-2π |
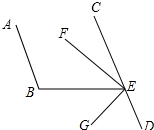 如图,已知AB∥CD,∠B=96°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数.
如图,已知AB∥CD,∠B=96°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数.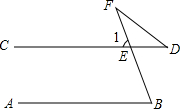 如图,AB∥CD,∠B=78°,∠D=32°,求∠F的度数.
如图,AB∥CD,∠B=78°,∠D=32°,求∠F的度数.