题目内容
8.已知△ABC中,∠A=30°.(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC=105°.
(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2,则∠BO2C=80°.
(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On-1(内部有n-1个点),求∠BOn-1C(用n的代数式表示).
(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On-1,若∠BOn-1C=60°,求n的值.

分析 (1)先根据三角形内角和定理求得∠ABC+∠ACB,再根据角平分线的定义求得∠OBC+∠OCB,即可求出∠BOC.
(2)先根据三角形内角和定理求得∠ABC+∠ACB,再根据三等分线的定义求得∠O2BC+∠O2CB,即可求出∠BO2C.
(3)先根据三角形内角和定理求得∠ABC+∠ACB,再根据n等分线的定义求得∠On-1BC+∠On-1CB,即可求出∠BOn-1C.
(4)依据(3)的结论即可求出n的值.
解答 解:∵∠BAC=30°,
∴∠ABC+∠ACB=150°,
(1)∵点O是∠ABC与∠ACB的角平分线的交点,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=75°,
∴∠BOC=105°;
(2)∵点O2是∠ABC与∠ACB的三等分线的交点,
∴∠O2BC+∠O2CB=$\frac{2}{3}$(∠ABC+∠ACB)=100°,
∴∠BO2C=80°;
(3)∵点On-1是∠ABC与∠ACB的n等分线的交点,
∴∠On-1BC+∠On-1CB=$\frac{n-1}{n}$(∠ABC+∠ACB)=$\frac{n-1}{n}$×150°,
∴∠BOn-1C=180°-$\frac{n-1}{n}$×150°
(4)由(3)得:180°-$\frac{n-1}{n}$×150°=60°,
解得:n=5.
点评 本题主要考查等分线的性质以及三角形内角和定理,根据题意找出规律是解题的关键.

练习册系列答案
相关题目
19.已知n是正整数,且$\sqrt{45n}$也是一个正整数,则正整数n的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 9 |
20.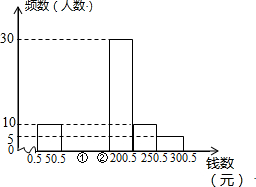 某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
(1)补全频数分布表和直方图;
(2)研究所认为,应对消费150元以上的学生提出勤俭节约的建议,试估计应对该校4000名学生中约多少名学生提出这项建议?
 某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.
某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成频数分布表和频数分布直方图.(1)补全频数分布表和直方图;
(2)研究所认为,应对消费150元以上的学生提出勤俭节约的建议,试估计应对该校4000名学生中约多少名学生提出这项建议?
| 分 组 | 频数 | 所占比例 |
| 0.5~50.5 | 10 | 0.1 |
| 50.5~100.5 | 20 | 0.2 |
| 100.5~150.5 | 35 | 35 |
| 150.5~200.5 | 30 | 0.3 |
| 200.5~250.5 | 10 | 0.1 |
| 250.5~300.5 | 5 | 0.05 |
| 合 计 | 100 | ------ |
17.下列计算正确的是( )
| A. | 3a+2b=5ab | B. | (a+2b)2=a2+4b2 | C. | a2•a3=a5 | D. | 4x2y-2xy2=2xy |
18.方程x2-5x=0的解是( )
| A. | x1=x2=5 | B. | x1=x2=0 | C. | x1=0,x2=5 | D. | x1=-5,x2=0 |
 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.
我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.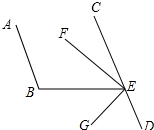 如图,已知AB∥CD,∠B=96°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数.
如图,已知AB∥CD,∠B=96°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数.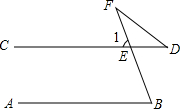 如图,AB∥CD,∠B=78°,∠D=32°,求∠F的度数.
如图,AB∥CD,∠B=78°,∠D=32°,求∠F的度数.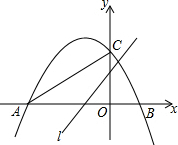 如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(-3,0),点B的坐标为(1,0),点C在y轴的正半轴上,且∠CAB=30°,若直线l:y=$\sqrt{3}$x+m从点C开始沿y轴向下平移.
如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(-3,0),点B的坐标为(1,0),点C在y轴的正半轴上,且∠CAB=30°,若直线l:y=$\sqrt{3}$x+m从点C开始沿y轴向下平移.