题目内容
一个两位数，若交换个位和十位的位置，则所得新两位数比原数小9，这个两位数十位和个位上的数字各是多少？（用方程）
考点：二元一次方程组的应用
专题：数字问题
分析：设这个两位数十位和个位上的数字各是x，y，根据题意列出方程，确定出这个两位数十位和个位上的数字即可．
解答：解：设这个两位数十位和个位上的数字各是x，y，
根据题意得：10x+y=10y+x+9，
整理得：9x=9y+9，即x=y+1，
∵2≤y+1≤9，
∴原来的两位数为21，32，43，54，65，76，87，98，
则这个两位数十位和个位上的数字分别为2，1；3，2；4，3；5，4；6，5；7，6；8，7；9，8．
根据题意得：10x+y=10y+x+9，
整理得：9x=9y+9，即x=y+1，
∵2≤y+1≤9，
∴原来的两位数为21，32，43，54，65，76，87，98，
则这个两位数十位和个位上的数字分别为2，1；3，2；4，3；5，4；6，5；7，6；8，7；9，8．
点评：此题考查了二元一次方程组的应用，弄清题意是解本题的关键．
练习册系列答案
出彩同步大试卷系列答案
相关题目
已知二次函数y=ax2+bx+c的图象如图所示，对称轴是直线x=1，下列结论中：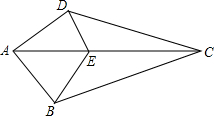
如图，已知，在四边形ABCD中，E是AC上一点，∠DAC=∠BAC，∠DCA=∠BCA．求证：∠DEC=∠BEC．
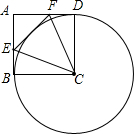在边长为6的正方形ABCD中，E是AB的中点，F在AD上，以C为圆心，CD为半径作⊙C，若EF=5，判断直线EF与⊙C的位置关系，并说明理由．
如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于D，若∠D=45°，则∠PCA=（ ）| A、50° | B、57.5° |
| C、60° | D、67.5° |
已知关于x的方程3x+a-8=0的解是x=2，则a的值是（ ）
| A、2 | B、3 | C、4 | D、5 |
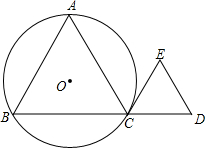已知点C是线段BD上一动点，分别以线段BC和线段DC为边在BD同侧作等边△ABC和等边△CDE，⊙O是△ABC的外接圆．