Question

如图，在△ABD和△ACE中，∠BAD=∠CAE=90°，AD=AE，AC=AE．
（1）求证：△ACD≌△AEB；
（2）试猜想：∠AFD和∠AFE的大小关系，试说明理由．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：（1）求出∠DAC=∠BAE，根据SAS推出两三角形全等即可；
（2）根据全等三角形的性质得出两三角形面积相等和DC=BE，根据面积公式求出AM=AN，根据角平分线性质得出即可．

解答：证明：（1）∵∠BAD=∠CAE=90°，
∴∠BAD+∠BAC=∠CAB+∠BAC，
∴∠DAC=∠BAE，
在△ACD和△AEB中，

AD=AB ∠DAC=∠BAE AC=AE

，
∴△ACD≌△AEB（SAS）；

（2）∠AFD=∠AFE，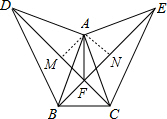
理由是：过A作AM⊥DC于M，AN⊥BE于N，
∵△ACD≌△AEB，
∴S_△ACD=S_△ABE，DC=BE，
∴

1

2

DC×AM=

1

2

BE×AN，
∴AM=AN，
∴∠AFD=∠AFE．

点评：本题考查了全等三角形的性质和判定，角平分线性质的应用，解此题的关键是推出△ACD≌△AEB，注意：到角两边距离相等的点在角的平分线上．