题目内容
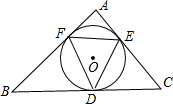 如图,△ABC的内切圆⊙O与各边相切于点D、E、F,且∠FOD=∠EOD=135°,则△ABC一定不是( )
如图,△ABC的内切圆⊙O与各边相切于点D、E、F,且∠FOD=∠EOD=135°,则△ABC一定不是( )| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
考点:三角形的内切圆与内心
专题:
分析:连结OE、OF、OD,如图,根据切线的性质得OD⊥BC,OE⊥AC,OF⊥AB,则∠ODB=∠OFB=90°,再根据四边形内角和计算出∠B=180°-∠FOD=45°,同理可得∠C=45°,于是可判断△ABC为等腰直角三角形.
解答:解: 连结OE、OF、OD,如图,
连结OE、OF、OD,如图,
∵△ABC的内切圆⊙O与各边相切于点D、E、F,
∴OD⊥BC,OE⊥AC,OF⊥AB,
∴∠ODB=∠OFB=90°,
∴∠B=180°-∠FOD=180°-135°=45°,
同理可得∠C=45°,
∴△ABC为等腰直角三角形.
故选B.
 连结OE、OF、OD,如图,
连结OE、OF、OD,如图,∵△ABC的内切圆⊙O与各边相切于点D、E、F,
∴OD⊥BC,OE⊥AC,OF⊥AB,
∴∠ODB=∠OFB=90°,
∴∠B=180°-∠FOD=180°-135°=45°,
同理可得∠C=45°,
∴△ABC为等腰直角三角形.
故选B.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.

练习册系列答案
相关题目
 如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.
如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式. 如图,菱形ABCD的边长为8cm,∠BAD=120°,半径为
如图,菱形ABCD的边长为8cm,∠BAD=120°,半径为 如图,⊙O的直径AB与弦CD相交于E,
如图,⊙O的直径AB与弦CD相交于E,
 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中: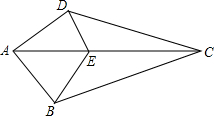 如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC=∠BEC.
如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC=∠BEC.