题目内容
3. AB是⊙O为弦,且AB=8,C为弧AB的中点,OC交AB于D,CD=2,则⊙O的半径等于5.
AB是⊙O为弦,且AB=8,C为弧AB的中点,OC交AB于D,CD=2,则⊙O的半径等于5.
分析 先根据C为弧AB的中点得出AB⊥OC,再根据垂径定理求出AD的长,设OA=r,则OD=r-CD=r-2,在Rt△AOD中根据勾股定理即可得出r的值.
解答 解:∵C为弧AB的中点,
∵AB⊥OC,
∵AB=8,
∴AD=$\frac{1}{2}$AB=4,
设OA=r,则OD=r-CD=r-2,
在Rt△AOD中,
∵OA2=AD2+OD2,即r2=42+(r-2)2,
解得:r=5.
故答案为:5.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
4.下列事件是必然事件的是( )
| A. | 若sinα=$\frac{\sqrt{2}}{2}$,则α=60° | |
| B. | 半径分别为3和5的两圆相外切,则两圆的圆心距为8 | |
| C. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 | |
| D. | 在反比例函数y=$\frac{1}{x}$的图象上,y随着x的增大而减小 |
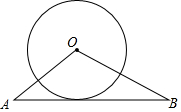 如图,已知在△OAB中,OA=OB=13,AB=24,⊙O的半径长为r=5,判断直线AB与⊙O的位置关系,并说明理由.
如图,已知在△OAB中,OA=OB=13,AB=24,⊙O的半径长为r=5,判断直线AB与⊙O的位置关系,并说明理由.
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为$\frac{18}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为$\frac{18}{5}$.