题目内容
6.在△ABC中,AB=AC,BD是高.若∠ABD=40°,则∠C的度数为65°.分析 首先在直角△ABD中,利用三角形内角和定理求得∠A的度数,然后利用三角形内角和定理求得∠ABC的度数.
解答  解:在直角△ABD中,∠A=90°-∠ABD=90°-40°=50°,
解:在直角△ABD中,∠A=90°-∠ABD=90°-40°=50°,
∵AB=AC,
∴∠ABC=∠C,
∴∠C=∠ABC=$\frac{180°-∠A}{2}$=$\frac{180°-50°}{2}$=65°.
故答案为:65°.
点评 此题考查了等腰三角形的性质,三角形的内角和定理,熟练掌握等腰三角形性质是解题的关键.

练习册系列答案
相关题目
17.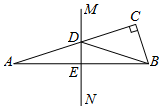 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A为( )
如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A为( )
 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A为( )
如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD:∠DBA=3:1,则∠A为( )| A. | 18° | B. | 20° | C. | 22.5° | D. | 30° |
14.以下数值反映数据的波动性特征的是( )
| A. | 均值 | B. | 众数 | C. | 方差 | D. | 中位数 |
11.下列点中,一定在二次函数y=x2-1图象上的是( )
| A. | (0,0) | B. | (1,1) | C. | (1,0) | D. | (0,1) |
18.下列三个日常现象:
①用两根钉子就可以把一根木条固定在墙上; ②把弯曲的公路改直,就能够缩短路程;
③体育课上,老师测量某个同学的跳远成绩.
其中,可以用“两点之间,线段最短”来解释的现象是( )
①用两根钉子就可以把一根木条固定在墙上; ②把弯曲的公路改直,就能够缩短路程;
③体育课上,老师测量某个同学的跳远成绩.
其中,可以用“两点之间,线段最短”来解释的现象是( )
| A. | ①③ | B. | ②③ | C. | ① | D. | ② |
15.地球距太阳约为150000000km,该数用科学记数法表示为( )
| A. | 15×107 | B. | 0.15×109 | C. | 1.5×108 | D. | 150×106 |

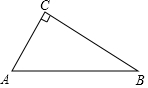 如图,在Rt△ACB中,∠C=90°,∠A=60°,AB=8.点P是AB边上的一个动点,过点P作PD⊥AB交直角边于点D,设AP为x,△APD的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,在Rt△ACB中,∠C=90°,∠A=60°,AB=8.点P是AB边上的一个动点,过点P作PD⊥AB交直角边于点D,设AP为x,△APD的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )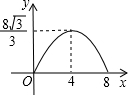

 AB是⊙O为弦,且AB=8,C为弧AB的中点,OC交AB于D,CD=2,则⊙O的半径等于5.
AB是⊙O为弦,且AB=8,C为弧AB的中点,OC交AB于D,CD=2,则⊙O的半径等于5.