题目内容
15.我校某班45名同学参加紧急疏散演练,对比发现:经专家指导后,平均每秒撤离的人数是指导前的3倍,这45名同学全部撤离的时间比指导前快30秒.求指导前平均每秒撤离的人数.分析 首先设指导前平均每秒撤离的人数为x人,则经专家指导后,平均每秒撤离的人数是3x人,根据“这45名同学全部撤离的时间比指导前快30秒”可得等量关系:45人在被专家指导前撤离所用的时间-45人在被专家指导后撤离所用的时间=30秒,由等量关系列出方程,解方程即可.
解答 解:设指导前平均每秒撤离的人数为x人,由题意得:
$\frac{45}{x}$-$\frac{45}{3x}$=30,
解得:x=1,
经检验:x=1是原分式方程的解,
答:指导前平均每秒撤离的人数为1人.
点评 此题主要考查了分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.列分式方程解应用题的一般步骤:审、设、列、解、验、答.必须严格按照这6步进行做题,规范解题步骤,另外还要注意完整性:如设和答叙述要完整,要写出单位等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列三个日常现象:
①用两根钉子就可以把一根木条固定在墙上; ②把弯曲的公路改直,就能够缩短路程;
③体育课上,老师测量某个同学的跳远成绩.
其中,可以用“两点之间,线段最短”来解释的现象是( )
①用两根钉子就可以把一根木条固定在墙上; ②把弯曲的公路改直,就能够缩短路程;
③体育课上,老师测量某个同学的跳远成绩.
其中,可以用“两点之间,线段最短”来解释的现象是( )
| A. | ①③ | B. | ②③ | C. | ① | D. | ② |
19.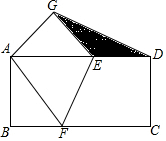 如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )
如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )
 如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )
如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )| A. | 5 | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
4.若函数y=$\left\{\begin{array}{l}{{x}^{2}-2(x≤2)}\\{2x(x>2)}\end{array}\right.$,则当函数值y=8时,自变量x的值是( )
| A. | ±$\sqrt{6}$ | B. | 4 | C. | ±$\sqrt{6}$或4 | D. | 4或-$\sqrt{6}$ |
 AB是⊙O为弦,且AB=8,C为弧AB的中点,OC交AB于D,CD=2,则⊙O的半径等于5.
AB是⊙O为弦,且AB=8,C为弧AB的中点,OC交AB于D,CD=2,则⊙O的半径等于5.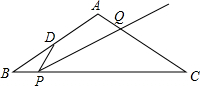 如图,等腰△ABC中,AB=AC=4,BC=m,点D是边AB的中点,点P是边BC上的动点,且不与B、C重合,∠DPQ=∠B,射线PQ交AC于点Q.当点Q总在边AC上时,m的最大值是4$\sqrt{2}$.
如图,等腰△ABC中,AB=AC=4,BC=m,点D是边AB的中点,点P是边BC上的动点,且不与B、C重合,∠DPQ=∠B,射线PQ交AC于点Q.当点Q总在边AC上时,m的最大值是4$\sqrt{2}$.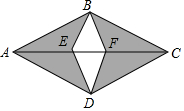 如图是某房间木地板的一个图案,其中AB=BC=CD=DA,BE=DE=DF=FB,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.若房间的面积是23m2,问最少需要有花纹的三角形木块和无花纹的木块各多少块?
如图是某房间木地板的一个图案,其中AB=BC=CD=DA,BE=DE=DF=FB,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.若房间的面积是23m2,问最少需要有花纹的三角形木块和无花纹的木块各多少块? 如图所示:在长方形中放置了6个正方形,图中给出了相关数据,请你仔细观察图形,利用方程思想求出图中的阴影部分的面积的和.
如图所示:在长方形中放置了6个正方形,图中给出了相关数据,请你仔细观察图形,利用方程思想求出图中的阴影部分的面积的和.