Question

13．如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB交于点D，则AD的长为$\frac{18}{5}$．

Answer 1

分析 首先过点C作CE⊥AD于点E，由∠ACB=90°，AC=3，BC=4，可求得AB的长，又由直角三角形斜边上的高等于两直角边乘积除以斜边，即可求得CE的长，由勾股定理求得AE的长，然后由垂径定理求得AD的长．

解答 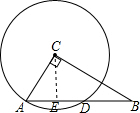解：过点C作CE⊥AD于点E，
则AE=DE，
∵∠ACB=90°，AC=3，BC=4，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5，
∵S_△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CE，
∴CE=$\frac{AC•BC}{AB}$=$\frac{12}{5}$，
∴AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=$\frac{9}{5}$，
∴AD=2AE=$\frac{18}{5}$，
故答案为$\frac{18}{5}$．

点评 本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．